Обращенный базис и симплекс-множители

Рассмотрим решение ЗЛП с точки зрения линейной алгебры. В матричном виде каноническая форма ЗЛП имеет вид:

, где ,

.

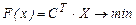Представим матрицу A в виде «склеенных» двух матриц . Здесь матрица – матрица, состоящая из столбцов матрицы A, соответствующих переменным, которые в оптимальной таблице являются базисными. Матрица состоит из всех оставшихся столбцов. Предположим, известна матрица B^–1. Умножим слева ограничения ЗЛП на матрицу B^–1:

, здесь 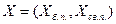, следовательно,

, следовательно, , .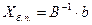

В невырожденном допустимом базисном решении (НДБР) базисным переменным соответствует единичная матрица, то есть . Так как A умножается на B^–1, то , что соответствует матрице коэффициентов оптимальной таблицы. Следовательно, в оптимальной таблице в столбцах тех переменных, которые были базисными в НДБР находится матрица B^–1.

Определение 4.1. Матрица, находящаяся в оптимальной таблице среди коэффициентов ограничений, стоящих в столбцах тех переменных, которые были базисными в исходной таблице, называется обращенным базисом и обозначается B^–1.

Запишем ЗЛП в канонической форме с предпочтительными переменными:

.

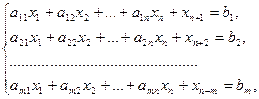
Умножим каждое ограничение на некоторое число 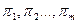соответственно и сложим с выражением целевой функции, тогда получим:

. (4.1)

Значения можно подобрать таким образом, чтобы коэффициенты перед базисными переменными равнялись нулю. Без ограничения общности, например, первые m переменных являются базисными, тогда можно определить из системы:

.

Если предположить, что подобрали таким образом, что перед базисными переменными коэффициенты равны 0, а перед свободными – неотрицательны, то вид (4.1) будет соответствовать оптимальному виду таблицы. Следовательно, в оптимальной таблице коэффициенты в выражении целевой функции перед переменными, которые были базисными в исходной таблице, есть , при этом .

Определение 4.2. Симплекс-множители – это такие числа 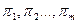, при умножении на которые каждого ограничения соответственно и сложении с выражением целевой функции будет получен такой вид целевой функции, что перед базисными переменными коэффициенты равны нулю, а перед свободными – неотрицательны.

Замечание 4.1. Если не все коэффициенты свободных переменных в выражении целевой функции неотрицательны, то это симплекс-множители промежуточного решения.