Правила построения двойственной ЗЛП

Существует много различных комбинаций ограничений и целевой функции для записи исходной задачи. Для упрощения задачи построения двойственной ЗЛП запишем прямую задачу в стандартном виде:

,

.

Правила построения двойственной ЗЛП:

1) Если прямая задача решается на максимум, то двойственная – на минимум, и наоборот.

2) В задаче на максимум ограничения-неравенства имеют смысл , а в задаче на минимум – .

3) Каждому ограничению прямой задачи соответствует переменная двойственной задачи, и наоборот.

4) Матрица системы ограничений двойственной задачи получается из матрицы системы ограничений исходной задачи транспонированием.

5) Свободные члены системы ограничений прямой задачи являются коэффициентами при соответствующих переменных целевой функции двойственной задачи, и наоборот.

6) Если на переменную прямой задачи наложено условие неотрицательности, то соответствующее ограничение двойственной задачи записывается как ограничение-неравенство, если же нет, то как ограничение-равенство.

7) Если какое-либо ограничение прямой задачи записано как равенство, то на соответствующую переменную двойственной задачи условие неотрицательности не налагается.

Пример. К данной ЗЛП составить двойственную задачу:

.

Преобразуем исходную ЗЛП к стандартному виду с максимизацией целевой функции:

.

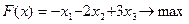Составим двойственную ЗЛП по ранее указанным правилам:

.

Основные теоремы двойственности и их экономическое содержание

Теоремы двойственности позволяют установить взаимосвязь между оптимальными решениями пары двойственных задач. Решив одну из пары двойственных задач, можно или найти оптимальное решение другой задачи, не решая ее, или установить его отсутствие. Возможны следующие случаи:

1) обе задачи из пары двойственных задач имеют оптимальные решения;

2) одна из задач не имеет решения ввиду неограниченности целевой функции, а другая – ввиду несовместности системы ограничений.

Теорема 5.1. (Основное неравенство теории двойственности)Для всех допустимых планов x и y пары взаимно двойственных задач справедливо неравенство F(x) ≤ Z(y).

Его экономическое содержание состоит в том, что для любого допустимого плана производства x и любого допустимого вектора оценок ресурсов y, общая созданная стоимость не превосходит суммарной оценки ресурсов.

Теорема 5.2. (Достаточный признак оптимальности) Если для некоторых допустимых планов x* и y* пары двойственных задач выполняется равенство F(x*)=Z(y*), то x* и y* являются оптимальными планами соответствующих задач.

Экономический смысл критерия: план производства x и вектор оценок ресурсов y являются оптимальными, если цена всей произведенной продукции и суммарная оценка ресурсов совпадают.

Теорема 5.3. (Существование оптимальных планов пары двойственных задач) Для существования оптимального плана каждой из пары двойственных задач необходимо и достаточно существование допустимого плана для любой из них.

Теорема 5.4. Если одна из двойственных задач имеет оптимальное решение, то и другая имеет оптимальное решение, причем экстремальные значения целевых функций совпадают, то есть F(x*)=Z(y*). Если одна из двойственных задач неразрешима, вследствие неограниченности целевой функции на множестве допустимых решений, то система ограничений другой задачи противоречива.

Экономическое содержание теоремы:если задача определения оптимального плана, максимизирующего выпуск продукции, разрешима, то разрешима и задача определения оценок ресурсов, причем цена продукта полученного в результате реализации оптимального плана совпадает с суммарной оценкой ресурсов.

Связь между задачами двойственной пары глубже, чем указано в формулировке теоремы: решая симплекс-методом одну из них, автоматически получаем решение другой. Для этого достаточно воспользоваться соответствием переменных прямой и двойственной задач и оценок в последней симплекс-таблице:

.

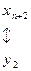
Теорема 5.5. Двойственная задача к двойственной есть прямая задача.

Теорема 5.6. Если пара двойственных задач имеет оптимальное решение, то при этом оптимальное значение переменных прямой задачи равно симплекс-множителям оптимального решения двойственной задачи, а значение переменных оптимального решения двойственной задачи равно симплекс-множителям оптимального решения прямой задачи.

Педагогический комментарий. Данное лекционное занятие закладывает основы для формирования следующих профессиональных умений студентов-экономистов: умение выявлять проблемы экономического характера при анализе конкретных ситуаций, предлагать способы их решения и оценивать ожидаемые результаты; умение разрабатывать и обосновывать варианты эффективных производственно-технологических решений; умение ставить цель и формулировать задачи, связанные с профессиональной деятельностью, умение использовать для их решения методы изученных дисциплин; умение логически мыслить; умение совершенствовать составление оперативно-производственного плана с использованием инструментария математического программирования; умение эффективно управлять экономическими процессами и регулировать использование комплекса имеющихся ресурсов; умение определять меру дефицитности ресурсов и оценку рентабельности или убыточности производимой продукции.

Тема 6. Элементы теории матричных игр

План лекции:

1. Основные понятия

2. Теоремы теории игр для парных матричных игр с нулевой суммой

3. Способы решения задач теории игр (ТИ)

1. Основные понятия

В ТИ рассматриваются ситуации связанные с принятием решений, в которых два лица, принимающих решение, имеют конфликтующие цели. К числу типичных примеров относится рекламирование конкурирующих товаров и планирование военных стратегий противоборствующих армий.

Каждый из двух участников игрового конфликта, именуемый игроком, имеет некоторое множество (конечное или бесконечное) возможных выборов решения, которые называются стратегиями. Такие игры известны как парные игры с нулевой суммой, так как выигрыш одного игрока равен проигрышу другого.

При обозначении игроков через А и В с числом стратегий m и n соответственно игру обычно представляют в виде матрицы платежей игроку А:

A=

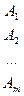
Такое представление матричной игры означает, что если игрок А использует стратегию i, а игрок В – j, то платеж игроку А составляет .

Определение 6.1. Ходом в игре называется принятие игроком на каждом ситуационном этапе определенного решения и выполнение на его основании действий, направленных на достижение поставленной этим игроком цели. Все допустимые альтернативные варианты хода игрока – стратегии.

Различают чистые и смешанные стратегии. Если очередной ход предписывается игроку однозначно (то есть вероятность осуществления такого хода равна 1), то стратегия называется чистой. Если же рекомендуется сделать ход с предписываемой вероятностью (0 < p < 1), то стратегия называется смешанной. Чистая стратегия, входящая в смешанную с ненулевой вероятностью, называется активной стратегией. Стратегия игрока называется оптимальной, если при многократном повторении игры она обеспечивает ему максимально гарантированный средний выигрыш или минимальный средний проигрыш.

Последовательность осуществленных ходов от начала игры до ее исхода называется партией игры.

Найти решение игры значит определить оптимальные стратегии игроков и цену игры, при этом первый игрок стремится обеспечить себе наибольший выигрыш, а второй – наименьший проигрыш.

Рассмотрим игру со следующей матрицей платежа:

А=

Определение 6.2. Нижней ценой игры (максимином) называется число 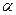, определяемое по формуле:

.

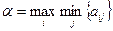Для указанной матрицы .

Определение 6.3. Верхней ценой игры (минимаксом) называется число определяемое по формуле:

.

Для указанной матрицы .

Стратегии игроков, соответствующие максимину (минимаксу), называются максиминными (минимаксными). Сумма выигрыша называется ценой игры и обозначается с.

В рассмотренной игре , что соответствует элементу матрицы . Элемент матрицы А, определяющий цену игры, называется седловой точкой, а сама игра – игрой с седловой точкой. В игре с седловой точкой оптимальное решение для каждого игрока – чистая стратегия. Решением рассмотренной задачи является .