
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Постановка ЗЛП. Различные формы записи ее математической модели
В общем виде ЗЛП формулируется следующим образом: максимизировать (минимизировать) функцию

 ,
,
при ограничениях:

где 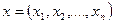 .
.
Рассмотрим матричную форму записи ЗЛП.
Введем следующие обозначения:
 ,
,  ,
,  ,
,  .
.
Следовательно,  и
и  .
. 
Различают следующие формы записи математической модели ЗЛП:
| Составные части модели | Формы записи математической модели ЗЛП | |||
| Общая | Стандартная | Каноническая | ||
| Ограничения | 
|

|

|

|
| Управляемые переменные | Произвольного знака |

|

| |
| Целевая функция |

|

|

|

|
Определение 1.10. Каноническая форма называется предпочтительной или с предпочтительными переменными, если в каждое уравнение ограничений входит некоторое  с коэффициентом +1, которого нет ни в одном другом уравнении ограничений и в целевой функции.
с коэффициентом +1, которого нет ни в одном другом уравнении ограничений и в целевой функции.
Определение 1.11. Если дополнительно в предпочтительной канонической форме свободные члены ограничений неотрицательны ( 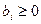 ), то канонический вид называется допустимым, в противном случае – недопустимым.
), то канонический вид называется допустимым, в противном случае – недопустимым.
Три формы записи ЗЛП (общая, стандартная, каноническая) эквивалентны в том смысле, что каждая из них с помощью несложных преобразований может быть сведена к другой форме.
При необходимости задачу минимизации можно заменить задачей максимизации, и наоборот, так как

(минимальное значение функции  равно максимальному значению функции
равно максимальному значению функции  , взятому с противоположным знаком, рис. 1.1).
, взятому с противоположным знаком, рис. 1.1).

Рис 1.1
Неравенства типа  путем умножения левых и правых частей на –1, можно преобразовать в неравенство типа
путем умножения левых и правых частей на –1, можно преобразовать в неравенство типа  , и наоборот.
, и наоборот.
Ограничения-неравенства  преобразуются в ограничения-равенства путем прибавления (вычитания) к левым частям дополнительных (балансовых) неотрицательных переменных
преобразуются в ограничения-равенства путем прибавления (вычитания) к левым частям дополнительных (балансовых) неотрицательных переменных 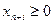 :
:
 .
.
В случае необходимости ограничение-равенство  , можно записать в виде системы-неравенств:
, можно записать в виде системы-неравенств:
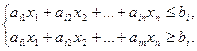
Если в ЗЛП какая-то переменная  не подчинена условию неотрицательности, ее заменяют разностью двух других неотрицательных переменных
не подчинена условию неотрицательности, ее заменяют разностью двух других неотрицательных переменных 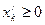 и
и  :
:
 .
.
Вводимые дополнительные переменные имеют определенный экономический смысл, прямо связанный с содержанием задачи.
Педагогический комментарий. Данное лекционное занятие закладывает основы для формирования следующих профессиональных умений студентов-экономистов: умение выявлять проблемы экономического характера при анализе конкретных ситуаций, предлагать способы их решения и оценивать ожидаемые результаты; умение ставить цель и формулировать задачи, связанные с профессиональной деятельностью, умение использовать для их решения методы изученных дисциплин; умение логически мыслить; умение реализовать комплекс связей экономических переменных и ограничений по ресурсам в форме математических моделей.
Тема 2. Графический метод решения ЗЛП. Закономерности и общие свойства решения ЗЛП
План лекции:
1. Геометрическая интерпретация решения ЗЛП
2. Алгоритм решения ЗЛП графическим методом
3. Возможные случаи области допустимых решений при решении ЗЛП
графическим методом
4. Основные свойства решения ЗЛП
5. Классификация решений ЗЛП
6. Решение ЗЛП с точки зрения линейной алгебры
Дата добавления: 2014-12-03; просмотров: 321; Мы поможем в написании вашей работы!; Нарушение авторских прав |