КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Многокритериальная оптимизация
Реальные ситуации бывают настолько сложными, что нередко приходиться учитывать несколько целевых функций, которые должны принимать экстремальные значения. Например, дать продукции больше, высокого качества и с минимальными затратами. Задачи, где находят решение по нескольким целевым функциям, относятся к задачам многокритериальной оптимизации. В процессе многокритериальной оптимизации формируется область согласований. В этой области любое решение нельзя улучшить ни по одному из критериев, не ухудшая его по какому-либо другому. Совокупность значений частных целевых функций в области согласования называется множеством Парето, а любое оптимальное состояние 
, где 
, для многокритериальной задачи называется оптимумом по Парето.
Основные понятия теории оптимизации
Определение 1.4. Функция 
, где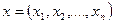 
имеет в точке 
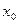- локальный экстремум, если существует двусторонняя окрестность этой точки, где для любого 
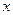этой окрестности будет выполняться: 1) 
в случае максимума; 2) 
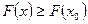в случае минимума. Если неравенства строгие, то экстремум называется сильным, если нестрогие – слабым.
Точки локального экстремума обязательно должны быть внутренними точками области Q определения функции 
.
Определение 1.5. Функция имеет в точке 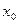области Q глобальный экстремум (оптимум), если неравенства выполняются для любой точки 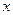из области Q.
Точка глобального экстремума может быть как внутренней, так и граничной точкой области Q.
Теорема 1.1. (Необходимое условие существования локального экстремума). Если функция 
имеет экстремум в точке 
, то 
, 
.
Теорема 1.2. (Достаточное условие существования локального экстремума). Если в точке все частные производные равны нулю, то, чтобы в этой точке функция имела экстремум, достаточно, чтобы квадратичная форма 
была положительно определенной для минимума и отрицательно определенной для максимума.
Определение 1.6. Квадратичная форма называется положительно определенной, если для любых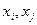 
, хотя бы одно из которых отлично от нуля, квадратичная форма принимает значение большее нуля.
Теорема 1.3. (Теорема Вейерштрасса). Непрерывная функция, определенная на непустом, замкнутом, ограниченном множестве, достигает экстремума, по крайней мере, в одной точке этого множества.
Определение 1.7. Множество S называется выпуклым, если отрезок, соединяющий любые две точки этого множества, целиком содержится в этом множестве.
Определение 1.8. Функция на выпуклом множестве S называется выпуклой, если ее график на любом отрезке 
целиком оказывается не выше хорды, соединяющей соответствующие точки графика (функция выпукла вниз) или не ниже этой хорды (функция выпукла вверх); в противном случае – функция не является выпуклой.
Теорема 1.4. Пересечение выпуклых множеств является выпуклым множеством.
Теорема 1.5. Сумма выпуклых функций является выпуклой функцией.
Теорема 1.6. (Основное свойство выпуклых функций). Любой локальный экстремум выпуклой функции является и глобальным, но не наоборот.
Определение 1.9. Вектор, указывающий направление наискорейшего возрастания функции, называется градиентом функции в соответствующей точке
.
Дата добавления: 2014-12-03; просмотров: 303; Мы поможем в написании вашей работы!; Нарушение авторских прав |