Геометрическая интерпретация решения ЗЛП

Геометрическая интерпретация экономических задач дает возможность наглядно представить их структуру, выявить особенности и открывает пути исследования более сложных свойств. ЗЛП с двумя переменными всегда можно решить графически, а с большим количеством – только при условии, что , где n – количество переменных, m – количество ограничений канонической записи ЗЛП.

Пусть дана задача:

.

Дадим геометрическую интерпретацию элементов этой задачи. Каждое из ограничений задает на плоскости некоторую полуплоскость (выпуклое множество). Пересечение любого числа выпуклых множеств является выпуклым множеством, следовательно, ОДР – выпуклое множество.

Примеры ОДР при решении ЗЛП графическим методом:

1) выпуклый многоугольник (рис. 2.1)

Рис. 2.1

2) неограниченная многоугольная область (рис.2.2)

Рис. 2.2

Перейдем к геометрической интерпретации целевой функции. Пусть ОДР ЗЛП – непустое множество А₁А₂А₃А₄А₅ (рис. 2.1). Выберем произвольное значение целевой функции F(x)=c, c=const. Следовательно,(2.1)– прямая линия.

Считая в равенстве (2.1) с параметром, получим уравнение семейства параллельных прямых, называемых линиями уровня целевой функции.

Как установить направление возрастания (убывания) целевой функции по и 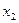? Частные производные 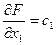и показывают скорости изменения 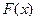вдоль осей и соответственно. Вектор – градиент целевой функции, показывает направление наискорейшего возрастания функции 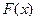. Вектор указывает направление наискорейшего убывания функции и называется антиградиентом. Градиент перпендикулярен к линиям уровня .