
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Примеры решения конструктивных задач
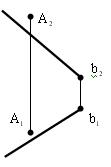
Пример 1 (рис. 8.12). Построить ВМТ, равноудалённых от двух заданных параллельных прямых а и b.
Решение.
Это плоскость  , проходящая через середину их общего перпендикуляра и перпендикулярно ему.
, проходящая через середину их общего перпендикуляра и перпендикулярно ему.
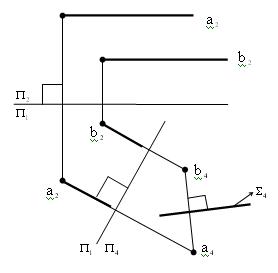
Рис. 8.12
Пример 2 (рис. 8.13). В заданной грани АВС построить ВМТ, равноудалённых от заданных точек М и К, расположенных вне плоскости  (АВС).
(АВС).
Решение.
Это прямая m – результат пересечения плоскости  (АВС) плоскостью
(АВС) плоскостью  , проходящей через середину отрезка МК перпендикулярно ему.
, проходящей через середину отрезка МК перпендикулярно ему.
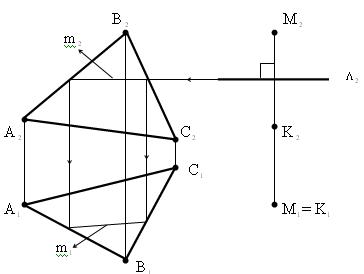
Рис. 8.13
Пример 3 (рис. 8.14). В плоскости  (А, b) через точку А провести прямую l под углом
(А, b) через точку А провести прямую l под углом  к плоскости проекций
к плоскости проекций 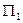 .
.
Решение.
Всё множество прямых l, которые проходят через точку А под углом 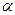 к плоскости
к плоскости 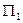 , есть конус вращения
, есть конус вращения 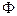 , у которого A
, у которого A 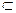 i
i 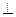
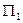 , угол ( l
, угол ( l 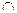
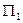 ) =
) = 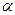 . Искомая прямая – одна из двух образующих l
. Искомая прямая – одна из двух образующих l 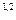 , являющихся результатом пересечения этого конуса
, являющихся результатом пересечения этого конуса 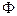 с плоскостью
с плоскостью  (A, b).
(A, b).
Дано:
Решение: 
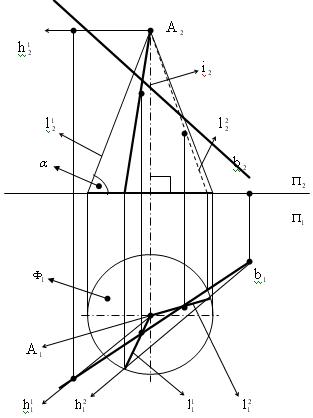
Рис. 8.14
Пример 4 (рис. 8.15). Построить ВМП, проходящих через заданную точку М и касательных к заданной сфере  .
.
Решение.
Это конус 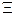 с вершиной в точке М и касательный к сфере
с вершиной в точке М и касательный к сфере 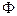 по линии m - окружности. Оси конуса и сферы совпадают: i
по линии m - окружности. Оси конуса и сферы совпадают: i 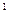 = i
= i 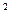 .
.
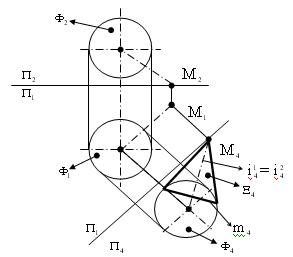
Рис. 8.15
Пример 5 (рис. 8.16). На прямой а определить точки, равноудалённые от заданной точки А на заданном расстоянии r .
Решение.
Это точки пересечения с прямой а окружности m радиусом r и с центром в точке А, лежащей в плоскости  (А, а).
(А, а).
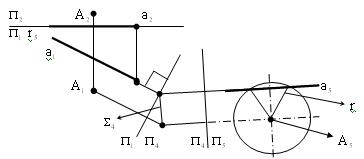
Рис. 8.16
9. Построение развёрток геометрических фигур
Развёртка – это плоская фигура, которую получают путём последовательного совмещения прямолинейных образующих развёртываемой фигуры с некоторой плоскостью.
Развёртки используют для раскроя листовых заготовок при изготовлении оболочковых изделий (химических аппаратов, ёмкостей, воздуховодов и т.п.).
9.1. Построение развёрток гранных поверхностей
Последовательность построения.
1.Определяют истинные величины всех сторон граней (для четырёхугольных граней дополнительно определяют их диагонали или высоты).
2.Используя полученные параметры граней, строят одну из них.
3.Последовательно к первой пристраивают все остальные грани.
Пример 1 (рис. 9.1). Построить развёртку пирамиды  (S,ABC).
(S,ABC).
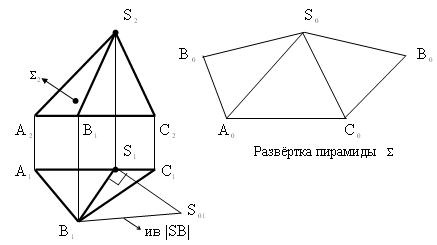
Рис. 9.1
Алгоритм построения.
1.Стороны основания пирамиды изображены на чертеже как отрезки горизонталей.
2.Рёбра SA и SC изображены на чертеже как отрезки фронталей.
3.Ребро SB определяем методом прямоугольника.
4.Развёртку начинаем с построения грани S  A
A 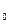 C
C 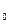 . Далее пристраиваем с обеих сторон грани S
. Далее пристраиваем с обеих сторон грани S 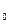 A
A 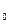 B
B 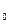 и S
и S 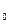 C
C 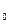 B
B 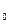 .
.
Пример 2 (рис. 9.2). Построить развёртку призмы  .
.
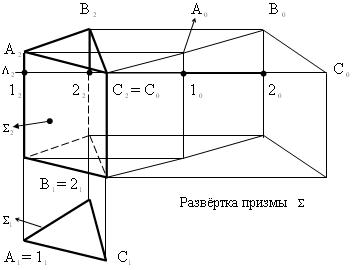
Рис. 9.2
Алгоритм построения.
1.Через точку С проведём секущую плоскость  (1,С,2) параллельно горизонтальной плоскости проекций, т.е. перпендикулярно рёбрам. Все стороны треугольника сечения 1С2 являются высотами соответствующих граней призмы и определены на чертеже как отрезки горизонталей. Рёбра призмы тоже определены на чертеже как горизонтально проецирующие отрезки.
(1,С,2) параллельно горизонтальной плоскости проекций, т.е. перпендикулярно рёбрам. Все стороны треугольника сечения 1С2 являются высотами соответствующих граней призмы и определены на чертеже как отрезки горизонталей. Рёбра призмы тоже определены на чертеже как горизонтально проецирующие отрезки.
2.Строим грань A  C
C  C
C 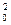 A
A 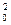 и пристраиваем к ней последовательно все остальные грани.
и пристраиваем к ней последовательно все остальные грани.
9.2. Построение развёрток кривых поверхностей
Среди кривых поверхностей есть развёртываемые (у них образующие – прямые линии) и не развёртываемые поверхности (например, сфера).
Пример 1 (рис. 9.3). Построить развёртку цилиндра вращения 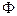 с радиусом окружности основания r и высотой h .
с радиусом окружности основания r и высотой h .
Алгоритм построения.
Поверхность развёртываема. Её развёртка представляет собой прямоугольник высотой h и с основанием, равным длине окружности основания цилиндра (2 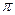 r).
r).
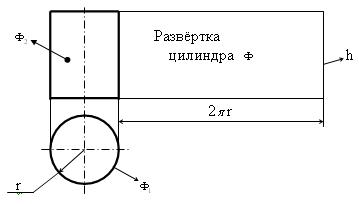
Рис. 9.3
Пример 2 (рис. 9.4). Построить развёртку конуса вращения 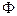 с радиусом окружности основания r и длиной образующей l .
с радиусом окружности основания r и длиной образующей l .
Алгоритм построения.
Поверхность развёртываема. Развёртка конуса вращения представляет собой сегмент (вершина S) радиусом R = l и с углом при вершине сегмента 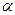 = 2
= 2 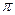 r / R (рад).
r / R (рад).
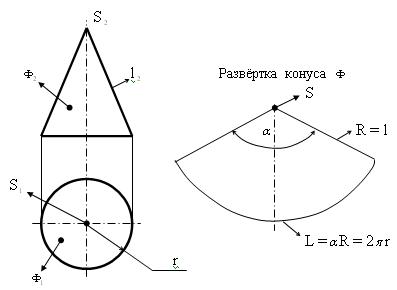
Рис. 9.4
Пример 3 (рис. 9.5). Построить развёртку конуса общего вида  , основание которого представляет собой горизонтально расположенную окружность m .
, основание которого представляет собой горизонтально расположенную окружность m .
Алгоритм построения.
Поверхность развёртываема, но поскольку образующие конуса имеют переменную длину, то для построения развёртки используют приближённый метод, при котором развёртка конуса заменяется развёрткой вписанной n-гранной пирамиды.
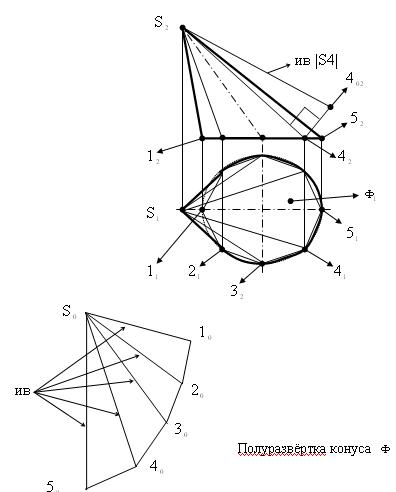
Рис. 9.5
Пример 4 (рис. 11.6). Построить развёртку цилиндра общего вида  , у которого плоскость одного основания (окружности) занимает горизонтальное положение, а плоскость другого – профильное.
, у которого плоскость одного основания (окружности) занимает горизонтальное положение, а плоскость другого – профильное.
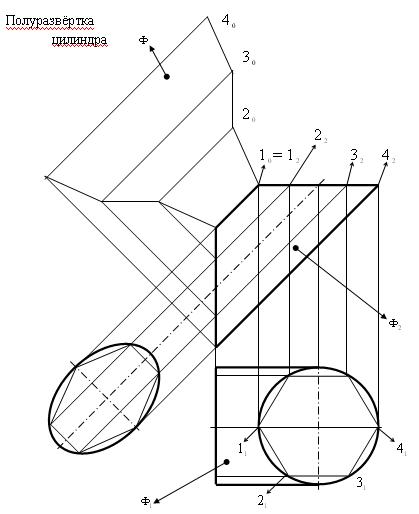
Рис. 9.6
Алгоритм построения.
Поверхность развёртываема. Однако образующие цилиндра имеют переменную длину, поэтому развёртку строят приближенным методом, заменяя развёртку цилиндра развёрткой вписанной в цилиндр n - гранной призмы.
Дата добавления: 2014-12-03; просмотров: 322; Мы поможем в написании вашей работы!; Нарушение авторских прав |