Оптимальный портфель, составленный из безрисковых активов и рискованных активов. Портфели с множеством рискованных активов.

Теперь рассмотрим комбинации риск — доходность, которые мы можем получить посредством объединения безрискового актива с рискованными активами 1 и 2, параметры которых остаются прежними, а безрисковая ставка доходности = 0,08.

На рис. 16 показано графическое представление всех возможных комбинаций риск — доходность. Кривая APDH есть кривая, изображенная на рис. 15, а прямая АН (рис. 16) представляет собой график, изображенный на рис. 14. Прямая показывает ряд комбинаций риск — доходность, которые могут быть получены посредством объединения безрискового актива с рискованным активом 1.

Рис. 16. Оптимальная комбинация рискованных активов

Прямая линия, соединяющая точку А с любой точкой кривой, соединяющей точки А_р ,D и H, представляет собой график, описывающий соотношение риск — доходность для всех комбинаций следующих трех активов: рискованных активов 1 и 2 с безрисковыми активами. Наибольшее значение этого соотношения, которое мы можем достичь, находится на линии, соединяющей точки А и К. Точка К является общей точкой прямой линии, выходящей из точки А, и кривой и, кроме того, это точка касания прямой и кривой. Исходя из этих условий формула для определения долей портфеля в точке К имеет вид

(26)

Такой рискованный портфель, который соответствует точке К на рис. 9, называется оптимальной комбинацией рискованных активов. Именно объединением этого портфеля рискованных активов с безрисковым активом достигается формирование максимально эффективного портфеля.

Хотя и другие рискованные эффективные портфели из модели Марковица могут быть скомбинированы с безрисковым активом, портфель заслуживает особого внимания, потому что не существует портфеля, состоящего из рискованных ценных бумаг, который, будучи соединен прямой линией с точкой, соответствующей безрисковому активу, лежал бы левее и выше его. Другими словами, из всех линий, которые могут быть проведены из точки, соответствующей безрисковому активу, и соединяют эту точку с рискованным активом или рискованным портфелем, ни одна не имеет больший наклон, чем линия, идущая в точку К.

Это важно потому, что часть эффективного множества модели Марковица отсекается этой линией. В частности, портфели, которые принадлежали эффективному множеству в модели Марковица и располагались между минимально рискованным портфелем и портфелем К, с введением возможности инвестирования в безрисковые активы не являются эффективными. Теперь эффективное множество состоит из прямого и искривленного отрезка. Прямой отрезок идет от безрискового актива в точку К и поэтому представляет портфели, составленные из различных комбинаций безрискового актива и портфеля К. Искривленный отрезок расположен выше и правее точки К и представляет портфели из эффективного множества модели Марковица.

Подставляя данные в формулу (8), получаем:

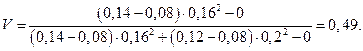
Это означает, что оптимальной комбинацией рискованных активов (для портфеля в точке касания с прямой, который еще называют тангенциальным портфелем), является 49% рискованного актива 1 и 51% рискованного актива 2. Ожидаемая ставка доходности и стандартное отклонение в точке К будут равны:

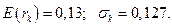
Тогда новый график для эффективного соотношения 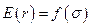будет иметь вид:

где угол наклона—отношение доходности к риску — равен 0,394. Для прежней прямой 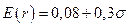угол наклона равен 0,30. Отсюда видно, что теперь инвестор находится в лучшем положении, потому что он может достичь более высокой ожидаемой ставки доходности для любого уровня риска, на который готов идти. Теперь обобщим относительно создания эффективного портфеля, когда имеются два вида рискованных активов и один безрисковой актив. Напомним, что предпочтения при формировании портфеля зависят от стадии жизненного цикла, на которой находится инвестор, периода (горизонта) планированности и отношения к риску. Следовательно, инвестор может выбрать позицию в любой точке на отрезке АК (рис. 16). На этом отрезке выбираем точку М, портфель, соответствующий этой точке, на 50% состоит из портфельных инвестиций в общей точке К (тангенциальный портфель) и на 50% из инвестиций в безрисковый актив.

Преобразуем уравнение (20) и (21) таким образом, чтобы они отражали тот факт, что портфель в точке касания А является теперь единственным рискованным активом, который следует объединить с безрисковым активом. Находим

Учитывая, что тангенциальный портфель состоит на 49% из рискованного актива 1 и на 51% — из рискованного актива 2, и на долю рискованных активов приходится 50% всего портфеля, определяем, что в портфеле будет 0,5 • 49% = 24,5% рискованных активов 2. Таким образом, состав портфеля М будет следующим: доля безрискового актива составляет 50%, доля рискованного актива 1 — 24,5% и доля рискованного актива 2 — 25,5%.

Следовательно, если вы инвестировали 10000 у.е. в портфель М, то 5000 у.е. инвестировано в безрисковый актив, 2450 у.е. — в рискованный актив 1 и 2550 у.е. — в рискованный актив 2.

Таким образом, существует только один портфель с рискованными активами, который оптимальным образом можно объединить с безрисковым активом. Этот портфель мы назовем оптимальной комбинацией рискованных активов, соответствующий общей (касательной) точке К. Следовательно, предпочтительный портфель всегда является комбинацией портфеля рискованных активов в общей точке и безрискового актива.

Важно отметить, что при поиске оптимальной комбинации рискованных активов нам не нужно ничего знать ни о благосостоянии инвестора, ни о его предпочтениях. Состав этого портфеля зависит только от ожидаемых ставок доходности и стандартных отклонений рискованного актива 1 и рискованного актива 2 и от корреляции между ними. Это означает, что все инвесторы, которые согласились на такие характеристики доходности (среднее значение, стандартное отклонение, корреляция), захотят инвестировать в один и тот же тангенциальный портфель, дополненный безрисковым активом. Вот общее правило, применимое ко всем случаям, когда имеется множество рискованных активов. Всегда существует оптимальный портфель рискованных активов, который все инвесторы, избегающие риска и имеющие одинаковые представления о характеристиках доходности, будут объединять с безрисковым активом с целью получения наиболее предпочтительного портфеля.

При наличии большого числа рискованных активов мы используем двухэтапный метод создания портфеля, аналогичный тому, который был рассмотрен в предыдущем разделе. На первом этапе мы рассматриваем портфели, состоящие только из рискованных активов, а на втором этапе мы определяем тангенциальный портфель рискованных активов, который можно объединить с безрисковым активом. Такая работа требует большого количества вычислений, поэтому лучше выполнять ее на компьютере. [Боди Зви, Мертон Роберт. Финансы / Пер. с англ. — М.: ИД «Вильяме», 2000.]

Вернемся к вопросу, каким образом финансовый посредник (например, компания, предлагающая инвесторам инвестиции в управляемые ею взаимные фонды) составляет «финансовое меню» из разных комбинаций активов, чтобы предложить его своим клиентам? Мы только что показали, что нахождение оптимальных комбинаций рискованных активов зависит только от ожидаемого уровня доходности, стандартных отклонений базовых рискованных активов и от корреляции между ними. Оно не зависит от предпочтений инвесторов. Следовательно, для того, чтобы создать эффективный портфель, сведения о предпочтениях инвесторов совершенно не нужны.

Итак, клиенты возлагают на финансовых посредников, которые специализируются на соответствующих видах деятельности, составление прогноза ожидаемого уровня доходности активов, стандартных отклонений и корреляции; посредники берут на себя также функцию комбинирования базовых активов в оптимальных пропорциях. Следовательно, клиентам остается только выбрать размеры капиталов, которые они намерены вложить в оптимальный рискованный портфель.

Статистическая модель выбора активов для инвестиционного портфеля, опирающаяся на среднее значение доходности и ее дисперсию, заложила теоретические основы финансового посредничества взаимных фондов. Начиная с конца 60-х годов академические исследования в области составления оптимального портфеля вышли за пределы этой модели и занялись динамическими версиями. В них межвременная оптимизация решений инвесторов относительно сбережения — потребления, принимаемых на определенных стадиях жизненного цикла домохозяйства, объединяется с распределением высвободившихся сбережений среди альтернативных направлений инвестиций. В этих моделях спрос на индивидуальные активы зависит от более серьезных факторов, нежели достижение оптимальной диверсификации, как было показано выше. Он является также следствием желания хеджировать различные риски, не включенные в первоначальную модель. В число рисков, которые создают потребность в хеджировании при принятии решений о составе портфеля, входят риск смерти, риск случайных изменений процентных ставок и ряд других. Динамические модели значительно обогатили теоретические воззрения на роль ценных бумаг и финансовых посредников при формировании инвестиционного портфеля.

В практике управления активами в рамках инвестиционного менеджмента по-прежнему преобладает базовый метод оценки риска на основании вычисления средней доходности и дисперсии портфеля (mean-variance approach). Однако все меняется. Благодаря более совершенным моделям составления портфеля инвестиционные компании теперь могут предлагать клиентам не просто оптимальные комбинации рискованных и безрисковых активов, а целое «семейство» взаимных фондов. Эти дополнительные фонды позволяют создавать оптимальные хеджинговые портфели, рассчитанные на еще более полное удовлетворение запросов самых разных клиентов. Инвестиционная компания может создавать из своих взаимных фондов интегрированные продукты, объединяя разные комбинации своих фондов в пропорциях, которые соответствуют запросам клиентов на разных стадиях их жизненных циклов.