Портфель Марковича максимальной эффективности. Решение задачи о максимально полезном портфеле.

Постановку Марковица задачи формирования оптимального портфеля (15) — (17) можно словами сформулировать так: сформировать портфель минимального риска из всех портфелей, имеющих эффективность не менее заданной.

Но столь же естественна и задача формирования портфеля максимальной эффективности из всех портфелей, имеющих риск не более заданного:

Найти , максимизирующие ожидаемую эффективность портфеля

при условии, что обеспечивается заданное значение риска портфеля, т.е. поскольку — доли, то в сумме они должны составлять единицу.

Назовем данную формализацию портфелем Марковица максимальной эффективности.

Решая задачу Марковица (15) — (17) для различных значений Е_р, получим множество точек . В плоскости портфельных характеристик Е_р, найденным эффективным точкам будет соответствовать соединяющая их кривая, называемая траекторией эффективных портфелей (рис. 11)

Рис. 11.Зависимость минимального риска от ожидаемой эффективности портфеля

Отметим, что, во-первых, множество эффективных портфелей составляет подмножество множества допустимых портфелей и, во-вторых, что на эффективной траектории допустимые портфели являются одновременно и эффективными в том смысле, что они дают минимальный риск при фиксированной ожидаемой доходности или максимальную ожидаемую доходность при данном риске.

Согласно сформулированным выше принципам теории Марковица, инвестор всегда выбирает портфель, лежащий на эффективной границе. Этот выбор осуществляется посредством анализа соотношения риска и доходности (постоянного «взвешивания»). Двигаясь вдоль границы слева направо, мы увеличиваем ожидаемый риск, но при этом расширяются и границы доходности. В связи с этим возникает следующий вопрос: какой же портфель лучше? Лучший из всех портфелей на эффективной границе Марковица называется оптимальным.

Интуитивно понятно, что оптимальный портфель зависит от предпочтений инвестора при выборе между риском и доходностью. Как уже говорилось в начале главы, эти предпочтения можно описать при помощи функции полезности.

На рис. 12 изображены три кривые безразличия и эффективная граница. В нашем случае кривая безразличия определяет комбинации риска и ожидаемой доходности, дающие одинаковый уровень полезности. И чем дальше расположена кривая от горизонтальной оси, тем больше полезность.

Также из рис. 12 видно, какой портфель при данных кривых безразличия будет для инвестора оптимальным. Следует помнить, что инвестор стремится к самой высокой кривой безразличия, какую можно достичь на эффективной границе. При этих требованиях оптимальный портфель представлен точкой пересечения кривой безразличия с эффективной границей. На рис. 12 это портфель А. Инвестор находит точку А , в которой полезность максимальна, и вслед за этим устанавливает оптимальный для себя портфель как решение X* задачи (15) — (17).

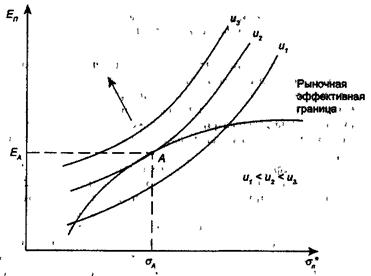
Рис. 12.Выбор оптимального портфеля

Портфель А максимизирует полезность для определенных характером кривой безразличия предпочтений риска и доходности инвестора, а также его ожиданий по поводу доходности и ковариации. Если его предпочтения относительно ожидаемого риска и доходности изменятся, изменится и оптимальный портфель. Например, на рис. 13 изображена та же эффективная граница, но другие кривые безразличия. В этом случае оптимальным будет портфель В с более низкими доходностью и риском, чем портфель А на рис. 12.

Рис. 13.Выбор оптимального портфеля при других кривых безразличия

При этом может возникнуть вопрос о том, как определить функцию полезности инвестора, чтобы построить его кривую безразличия? К сожалению, ответить на него непросто. Дело в том, что экономисты еще не пришли к единому мнению о том, как измерять полезность.

Это, однако, не означает, что теория бесполезна. А говорит лишь о том, что, описав эффективную границу, инвестор должен определить, какой эффективный портфель ему подходит в наибольшей степени.

Мы рассматривали вопрос о влиянии диверсификации вклада на снижение риска и получили формулу (14)

которая показывает, что при росте числа п видов ценных бумаг, включаемых в портфель, риск эффективного портфеля ограничен и стремится к нулю при .

Отсюда вытекает главное практическое правило финансового рынка: для повышения надежности эффекта от вклада в рискованные ценные бумаги целесообразно делать вложения не в один их вид, а составлять портфель, содержащий возможно большее разнообразие ценных бумаг, эффект от которых случаен, но случайные отклонения независимы.

Однако в реальности большого разнообразия достичь трудно, поскольку гипотеза независимости эффектов в достаточной степени условна и ограничивает возможности подобного расширения: технологическая сопряженность и экономическая взаимозависимость хозяйствующих субъектов естественным образом проявляются в статистическом взаимодействии случайных эффективностей ценных бумаг.

Отметим также, что с практической точки зрения выгоды от масштабной диверсификации далеко не бесспорны: ее экономически обоснованные размеры ограничиваются влиянием трансакционных издержек. С ростом числа сделок эти издержки делают включение в портфель малых партий большого числа активов неоправданно дорогим занятием.

Анализ, проведенный экономистами США, показал, что значительную часть диверсифицируемого риска можно устранить, включая в портфель около 20 видов ценных бумаг, и дальнейшее увеличение числа видов таких активов в портфеле ведет к существенному падению темпа уменьшения риска. Кривая риска индивидуального портфеля 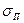при увеличении числа активов асимптотически приближается к уровню риска рыночного портфеля (рис. 14).

Из описания теории Марковица, можно сделать вывод, что она дает принципы построения эффективных портфелей и способы выбора из них наилучшего, или оптимального, портфеля. Эта теория отличается от предыдущих тем, что в ней сформулированы принципы измерения основных параметров теории. К ним относятся риск и ожидаемая доходность как отдельных активов, так и всего портфеля в целом. Более того, при помощи этих величин, а также ковариации и корреляции между доходностями активов можно осуществить диверсификацию портфеля, цель которой состоит в уменьшении его риска без ущерба для доходности. Определение и точный смысл этих параметров основываются на теоретико-вероятностных понятиях, а их количественная оценка осуществляется статистическими методами.

Рис. 14. Зависимость риска портфеля от числа рисковых активов

Ожидаемая доходность портфеля — это взвешенное среднее ожидаемых доходностей всех активов, входящих в портфель. Вес каждого актива определяется как процентная доля рыночной стоимости актива в общей рыночной стоимости всего портфеля. Риск актива измеряется при помощи вариации или стандартного отклонения его доходности. В отличие от ожидаемой доходности портфеля его риск не равен взвешенному стандартному отклонению рисков отдельных активов, входящих в портфель. Риск портфеля зависит от ковариации и корреляции между активами. Чем ниже корреляция, тем меньше риск портфеля.

Эффективный портфель по Марковичу — это допустимый портфель с наибольшей ожидаемой доходностью для заданного уровня риска. Набор всех эффективных портфелей называется эффективным множеством портфелей, или эффективной границей.

Оптимальным портфелем называется такой портфель, который в наибольшей степени удовлетворяет предпочтениям инвестора по отношению к доходности и риску. Предпочтения инвестора описываются функцией полезности, которая графически представляется при помощи набора кривых безразличия. Оптимальный портфель — это такой портфель, для которого кривая безразличия касается эффективной границы.