Основные определения теории графов. 1. Сулицкий В.Н. Методы статистического анализа в управлении, «Дело», Москва, 2002

1. Сулицкий В.Н. Методы статистического анализа в управлении, «Дело», Москва, 2002

2. Гмурман В.Е. Теория вероятностей и математическая статистика.

3. Фомин Г. П. Математические методы и модели в коммерческой деятельности: Учебник. — 2-е изд., перераб. и доп. — М.: Финансы и статистика, 2005. — 616 с: ил

ЛЕКЦИЯ 5.1.

Основные определения

Основные определения теории графов

Неформально граф – это диаграмма, состоящая из кружков и линий, соединяющих кружки (рис.1). Кружки называются вершинами графа, а линии – ребрами. Такой граф называется неориентированным. Граф называется ориентированным (рис.2), если каждая линия снабжена стрелкой, показывающей допустимое направление движения от вершины к вершине. Ребро со стрелкой называется дугой.

Говорят, что задан неориентированный граф ,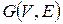

Если заданы

· Конечное множество , называемое множеством вершин графа

· Конечное множество , называемое множеством ребер графа

· Указано, какое ребро какие вершины соединяет.

Ребро 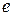называется петлей, если соединяет вершинуe с ней самое. Граф с петлями называется псевдографом. Ребра называются кратными, если соединяют одни и теже вершины. Граф с кратными ребрами называется мультиграфом. Граф без петель и кратных ребер называется простым графом. Всякое ребро однозначно определяет ту пару вершин, которая ему поставлена в соответствие, поэтому удобнее всего так ребро и обозначать - (или –, порядок перечисления вершин не имеет значения).

Мощность множества V – число вершин графа – обозначим буквой . Число ребер графа обозначим буквой .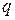

Проще всего вершины перенумеровать и обозначать каждую вершину её номером. Граф можно нарисовать, если вершины изображать кружками, а ребра – линиями, соединяющими соответствующие пары вершин. На рис. 1 показан простой граф с 4 вершинами и 5 ребрами.

Рис. 2

,

.

Говорят, что ребро инцидентно вершинам и и v, а вершины и и vинцидентны ребру . По-другому говорят, что ребро соединяет вершины и и v,авершины и и v являются концами ребра е.

Вершины, инцидентные одному и тому же ребру, называются смежными. Так же смежными называются ребра, инцидентные одной и той же вершине. Ясно, что бинарное отношение смежности – это симметричное бинарное отношение.

Множество вершин графа, смежных данной вершине v, обозначим ,

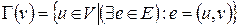
Если у ребра 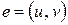выделяются первая вершина – вершина и втораявершина – вершина , ребро 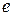становится ориентированным и называется дугой. Граф G с дугами вместо ребер называют ориентированным графом или орграфом. Тогда бинарное отношение уже не обязано быть антисимметричным, 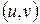и 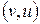– разные дуги.

Дугу 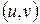на диаграмме изображают линией со стрелкой. Дуга ориентирована в направлении от вершины и (первой вершины упорядоченной пары 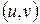) к вершине v(второй вершины упорядоченной пары ).

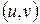Ребро заменяет собой две разнонаправленные дуги. Две стрелки на ребре, как правило, не рисуются. На рис. 2 показан ориентированный граф с множеством вершин и множеством дуг .

На рис. 3 показаны псевдограф и мультиграф. Кратные ребра мультиграфа соединяют одну и ту же пару вершин, концы петли соединяют одну и ту же вершину.

Рис. 3

В дальнейшем, если не будет оговорено противное, мы ограничимся рассмотрением простых графов.

Определение. Степенью 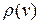вершины v неориентированного графа называется число ребер, инцидентных этой вершине. Вершина степени 0 называется изолированной; вершина степени 1 – висячей.

Множество вершин графа, смежных с данной вершиной , обозначим .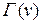

Утверждение. (Теорема Эйлера).Сумма степеней всех вершин данного графа равна удвоенному числу ребер графа

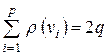
Доказательство.При подсчете суммы степеней вершин каждое ребро считается дважды, так как каждое ребро простого графа инцидентно ровно двум вершинам.

Следствие.Во всяком графе число вершин нечетной степени четно.

Доказательство. Если бы это было не так, то сумма степеней вершин графа оказалось бы нечетным числом, что невозможно.

Определение. Степенью 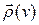выхода вершины v ориентированного графа называют число дуг, выходящих из этой вершины. Если 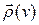= 0, то вершина v называется стоком.

Определение. Степенью входа вершины v ориентированного графа называют число дуг, входящих в эту вершину. Если = 0, то вершина v называется источником.