Матрица инцидентности неориентированного графа.

Пусть 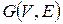– неориентированный граф с р вершинами и q ребрами. Произвольно переномеруем его вершины и ребра.

Определение. Матрицей инцидентности графа 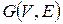называется матрица с р строками (каждая строка соответствует одной из вершин графа) и q столбцами (каждый столбец соответствует одному из ребер графа), элементы которой определяются правилом

Пример графа и его матрицы инцидентности приведен на рис. 11

Рис. 11

Свойства матрицы инцидентности неориентированного графа.

· Число единиц в i-й строке равно степени i-ой вершины, i = 1, 2, … , р.

· Число единиц в 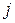-м столбце равно двум, так как любое ребро инцидентно двум вершинам, 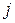= 1, 2, …, р.

· Число единиц в матрице равно удвоенному числу ребер графа.