
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
ПЕРВАЯ И ВТОРАЯ ФУНКЦИИ СЛОЖНОГО ПРОЦЕНТА
Первая функция сложного процента – это функция накопления денежной суммы за 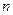 периодов времени при банковском проценте, равном
периодов времени при банковском проценте, равном 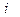 за один период. Ее называют [2] аккумулированной суммой денежной единицы.
за один период. Ее называют [2] аккумулированной суммой денежной единицы.
Пусть некоторая денежная сумма 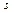 вкладывается вначале года в банк на
вкладывается вначале года в банк на 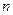 лет под процент
лет под процент 
Тогда к концу первого года накопление составит
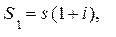
к концу второго года накопления сумма будет

а к концу 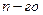 года
года
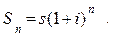 (1.1)
(1.1)
Величину

называют фактором аккумулированной (накопленной) суммы денежной единицы.
Вторая функция определяет накопление денежной единицы за определенный период.
Пусть этот период состоит из промежутков времени. Тогда денежная сумма 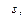 вложенная в начале первого промежутка будет приносить процент
вложенная в начале первого промежутка будет приносить процент 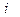 в течение
в течение 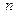 промежутков времени. Накопленная к концу периода сумма, вложенная в начале второго промежутка дает накопление
промежутков времени. Накопленная к концу периода сумма, вложенная в начале второго промежутка дает накопление  Такое накопление для последнего периода составит
Такое накопление для последнего периода составит  И вторая функция сложного процента будет иметь вид суммы:
И вторая функция сложного процента будет иметь вид суммы:
 (1.2)
(1.2)
Сумма (1.2) является суммой членов геометрической прогрессии, в которой знаменатель равен
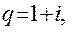 (1.3)
(1.3)
а первый член
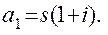 (1.4)
(1.4)
Сумма членов геометрической прогрессии имеет вид
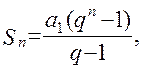 (1.5)
(1.5)
или с учетом (1.3), (1.4)
 (1.6)
(1.6)
Величину
 (1.7)
(1.7)
называют [2] фактором будущей стоимости авансового аннуитета, а сумму (1.6) – будущей стоимостью авансового аннуитета.
Слово аннуитет в данном случае следует понимать как доход (дословно с английского annuity – ежегодная рента).
Если сумма 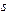 будет вноситься в конце промежутка времени, то вторая функция будет иметь вид такой суммы
будет вноситься в конце промежутка времени, то вторая функция будет иметь вид такой суммы
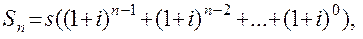
или
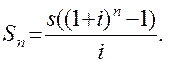 (1.8)
(1.8)
Величину (1.8) называют будущей стоимостью обычного аннуитета, а функцию
 (1.9)
(1.9)
фактором будущей стоимости обычного аннуитета.
Пример 1.1. Накапливаются деньги для покупки земельного участка с жилыми постройками. Они вкладываются по 100 у.е. в начале каждого месяца по 12% годовых, идущих ежемесячно. Такое накопление длится 5 лет (60 месяцев). Определить величину накопленной к концу срока суммы.
Решение: В данном примере  месяцев,
месяцев, 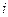 в расчете на каждый месяц составляет величину 0,12:12 = 0,01. Тогда в соответствии с (1.6)
в расчете на каждый месяц составляет величину 0,12:12 = 0,01. Тогда в соответствии с (1.6)
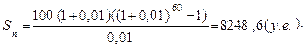
Дата добавления: 2014-12-03; просмотров: 334; Мы поможем в написании вашей работы!; Нарушение авторских прав |