Інтерференція хвиль

Узгоджене проходження в часі і просторі декількох коливань або хвильових процесів пов'язується з поняттям когерентності.

Дві хвилі називаються когерентними, якщо вони мають однакову частоту і різниця їх фаз залишається постійною в часі.

Інтерференцією хвиль називається явище, яке відбувається при накладанні двох або кількох когерентних хвиль, при якому має місце стійке в часі їх взаємне підсилення в одних точках простору і ослаблення в інших в залежності від співвідношення між фазами цих хвиль.

Розглянемо накладення двох плоских хвиль, які випромінюються точковими джерелами S₁ і S₂ (рис.1) з амплітудами А₁ і А₂ , частотами ω₁ і ω₂, хвильовими числами к₁ і к₂.

Рис. 1

Точкові джерела S₁ і S₂ випромінюють в напрямі точки М плоскі хвилі, рівняння яких мають вигляд

(5)

де r₁ і r₂ – відстані від джерел хвиль до точки М; к₁ і к₂ – хвильові числа; φ₁ і φ₂ – початкові фази обох хвиль; ω₁ і ω₂ – циклічні частоти хвиль.

Результуючу амплітуду при накладанні двох однаково направлених хвиль (5) знаходимо графічним методом (з допомогою векторної діаграми)

. (6)

Окремі випадки:

1. Нехай ω₁≠ ω₂, k₁≠k₂, φ₁≠φ₂.

В цьому випадку жодна складова правої сторони рівняння (6) не дорівнює нулю, а тому можна визначити лише середнє значення результуючої амплітуди. Оскільки середнє значення косинуса за час в один період дорівнює нулю, то

(7)

Рівняння (7) показує, що в цьому випадку в точці М відбувається просте додавання інтенсивностей (I ~ A²)

2. Нехай ω₁ = ω₂, k₁=k₂, φ₁= φ₂, A₁ = A₂ = A₀.

В цьому випадку рівняння (7) матиме вигляд

. (8)

Вираз під функцією косинуса в рівнянні (8) не залежить від часу , а тому не підлягає усередненню. Результуюча інтенсивність при накладанні двох хвиль в цьому випадку буде дорівнювати

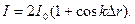(9)

Рівність (9) показує, що розподіл інтенсивності при накладанні двох хвиль з рівними циклічними частотами, хвильовими числами й початковими фазами в різних точках простору буде різною. Такі хвилі називаються когерентними, а явище називається інтерференцією.

Проведемо аналіз співвідношення (9).

1. Якщо kΔr =± 2nπ, де n = 1, 2, 3, … і k = ─ інтенсивність при накладанні двох когерентних хвиль буде дорівнювати

. (10)

Якщо в різниці ходу двох когерентних хвиль вкладається ціле число хвиль, то при їх накладанні інтенсивність зростає в 4 рази. Ця умова є умовою максимумів інтерференції, тобто

, де n = 0, 1, 2, 3, … ─ умова максимумів інтерференції.

2. Якщо kΔr = ± (2n +1) 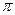, де n = 1, 2, 3, … і k = ─ інтенсивність при накладанні двох когерентних хвиль буде дорівнювати

(11)

Якщо в різниці ходу двох когерентних хвиль вкладається непарне число півхвиль, то при їх накладанні результуюча інтенсивність буде дорівнювати нулю. Ця умова є умовою мінімумів інтерференції, тобто

Δr= ±(2n+1) , де n=0, 1, 2, 3,… ─ умова мінімумів інтерференції.