Принцип накладання двох хвиль. Інтенсивність. Поняття когерентності хвиль

При накладанні довільних хвиль відбувається просте додавання їх інтенсивностей, тобто

(1)

У випадку когерентних хвиль, тобто хвиль однакових циклічних частот, амплітуд, хвильових чисел і сталої різниці фаз, інтенсивності хвиль не додаються, а перерозподіляються в просторі з утворенням максимумів і мінімумів. Таке явище в фізиці називається інтерференцією.

У випадку світлових хвиль перерахованих умов когерентності не завжди достатньо. Треба ще щоб вектори електромагнетних полів інтерферуючих хвиль коливались вздовж однакового напрямку, тобто, щоб інтерферуючі хвилі були поляризовані в одній площині.

Слід зауважити, що навіть співпадання векторів двох інтерферуючих хвиль ще не означає співпадання векторів цих хвиль. Ось чому практично не можливо побудувати ідеаьних джерел незалежної дії, які б давали в повній мірі когерентні промені. Останнім часом побудовані досить близькі до ідеальних, лазерні джерела. Такі джерела дають хвилі високої монохроматичності (однокорірності), а це означає і когерентності. Інтерференційна картина від лазерних променів (окремі лазери) є дещо спотворена порівняно з картиною інтерференції, одержаної від когерентних променів одного незалежного джерела.

Насамперед вияснимо, який з двох векторів і в електромагнетній хвилі, а це означає і світловій хвилі, є головним, або домінуючим.

На електрон який рухається в речовині з боку електромагнетного поля діє сила , яка дорівнює:

, (2)

де – сила, з якою діє на заряд електрона електрична складова електромагнетної хвилі; – магнетна складова сили.

Зупинимось дещо детальніше на природі магнетної складової сили, з якою електромагнетна хвиля діє на заряджену частинку. Вектор індукції магнетного поля виражаємо через вектор напруженості

. (3)

З теорії електромагнетних коливань (Лекція № 6) відомо, що

. (4)

З урахуванням (4) вираз (3) перепишеться:

. (5)

Значення індукції магнетного поля з (5) підставимо в (2)

. (6)

Однак , де 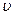– фазова швидкість електромагнетної хвилі, тому

(7)

Оцінимо величину швидкості електрона в атомі. Відомо, що при вимушених коливаннях електрона в атомі його амплітуда може досягати розмірів самого атома, а це величина, яка має порядок 10^{-10 м. Частота коливань для світлових променів має порядок 1015} Гц, тому

.

Фазова швидкість світла має порядок 10⁸ .

Поділимо величину електричної сили на величину магнетної сили, з якими світлові промені діють на електрони в атомі.

. (8)

Вектор електромагнетної хвилі за своєю дією перевищує в разів дію вектора .

З цих причин вектор електромагнетної хвилі вважають домінуючим, або світловим вектором. Коли говорять про поляризацію світлових променів, то мають на увазі коливання в певному напрямі лише вектора . Вектор теж коливається в певному напрямі, але в площині, яка є перпендикулярною до вектора .

Слід пам’ятати, що джерелами світлових хвиль є нагріті тіла, в яких атоми періодично збуджуються (рис. 1) і через час , повертаючись у нормальний стан, випромінюють кванти, або порції електромагнетних хвиль. За час збудженого стану випромінюється цуг, довжина якого l не перевищує 3 м.

, (9)

де – час збудженого стану; – швидкість світла.

Таким чином довжину окремого цугу можна вважати максимальною довжиною когерентності, а час – максимальним часом когерентності.

Рис. 1.

Реально інтерферують одночасно досить багато хвиль, які випромінюються величезною кількістю атомів. При цьому пучок променів не завжди строго когерентний. З цих причин довжина когерентності різко зменшується. Зменшується також час когерентності.

В такому реальному світловому пучку фаза хвиль здійснює випадкові зміни. Тому час когерентності визначається як час, протягом якого випадкова зміна різниці фаз хвиль досягає величини 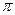. Такий час називається часом когерентності.

Відповідні розрахунки показують, що цей час пов’язаний з ступенем немонохроматичності реальних світлових променів, тобто:

, (10)

де – визначає розкид частот світлових хвиль в пучку.

Так як

, то або . (11)

З урахуванням (11) час когерентності (10) матиме вигляд

, (12)

де – довжина хвилі в пучку світла; – фазова швидкість світла; 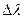– інтервал зміни довжин хвиль в пучку світла. Формула (12) визначає реальний час когерентності. Реальна довжина когерентності в цьому випадку буде дорівнювати

. (13)

Формула (13) показує, що довжина когерентності визначається ступенем немонохроматичності променів у пучку світла. Чим більш когерентні промені, тобто мале значення 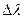, тим більша довжина когерентності.

Велика довжина когерентності лазерних променів пояснюється якраз високою монохроматичністю лазерного випромінювання.

Приклад. Пучок світла з довжиною хвиль від до використовують для одержання інтерференційної картини. Визначити для цього випромінювання довжину і час когерентності.

Важливо знати:

1. Відстань, яку проходять світлові промені між двома точками простору, називаються геометричним шляхом l.

2. Геометричний шлях, помножений на показник заломлення середовища, називається оптичним шляхом l_n.

3. Коли розглядають явище інтерференції світла, то мають на увазі лише оптичний шлях.

4. Інтерферують лише когерентні промені, оптична різниця ходу яких перебуває в межах довжини когерентності.

5. Промінь, який відбивається від оптично більш густого середовища (має більший показник заломлення ), змінює свою фазу на протилежну.

6. На межі з оптично менш густим середовищем зміни фази на протилежну при відбиванні світла не відбувається.

2. Інтерференція світла від двох когерентних джерел. Дослід Юнга

Ще в кінці 17 ст. Гюйгенс, вивчаючи фізичні процеси пов’язані з поширенням світла, встановив принцип, який дозволяв за відомим положенням хвильового фронту визначити його положення в наступні моменти часу. Цей принцип дістав назву принципу Гюйгенса.

Згідно принципу Гюйгенса будь-яка точка хвильової поверхні (поверхні однієї фази) може бути розглянута як вторинне точкове джерело світлових хвиль (рис.2).

Рис. 2.

Запропонований Гюйгенсом принцип дозволяє пояснити з хвильової точки зору закони відбивання і заломлення світла, а також механізм одержання когерентних хвиль в досліді Юнга.

Юнг здійснив такий дослід: малий отвір А (рис. 3) в непрозорому екрані освітлюється інтенсивним джерелом монохроматичного (одноколірного) світла. Згідно принципу Гюйгенса отвір А стає новим вторинним точковим джерелом світла. Це світло падає на два наступні малі отвори B₁ і B₂, які в свою чергу стають джерелами когерентних хвиль, так як утворені з однакових цугів.

Когерентні хвилі від двох вторинних точкових джерел світла B₁ і B₂ накладаються і на екрані E створюють інтерференційну картину з перерозподілом інтенсивності. В точці накладання хвиль буде спостерігатись максимум інтенсивності, якщо в оптичній різниці ходу цих хвиль буде вкладатись ціле число хвиль, або парне число півхвиль

; (14)

Якщо в різниці ходу двох хвиль вкладається непарне число півхвиль, то вони гасять одна одну, тобто спостерігається мінімум інтерференції

, (15)

де – порядок максимуму або мінімуму.

Рис. 2.

Розглянемо більш детально дослід Юнга. Нехай відстань між щілинами B₁ і B₂ дорівнює d, а відстань від щілин до екрана , причому . Позначимо відстань на екрані від нульового максимуму до точки утворення k-го максимуму через y_k (рис.4).

Рис. 4.

Якщо d і у_к набагато менші за L, то наближено одержимо

, (16)

Звідки

. (17)

Положення k-го максимуму на екрані можна одержати, якщо в (17) підставити із (14), тоді

. (18)

Для знаходження ширини інтерференційної полоси віднімаємо від у_к у_{к -1}

. (19)

Оскільки величини, які входять у формулу (19) є сталими, то ширина максимумів інтерференції теж є сталою величиною.

Ми розглянули приклад, коли дві хвилі від когерентних джерел (щілин) “поширюються” в однорідному середовищі з однаковою швидкістю. Однак в інших дослідах інтерферуючі хвилі можуть проходити різні середовища, і як наслідок мати різні фазові швидкості. У цьому випадку замість геометричної різниці ходу променів слід говорити про оптичну різницю ходу, тобто

(max), (20)

(min). (21)

При виведенні формул максимумів і мінімумів інтерференції від двох променів ми вважали, що щілини Юнга для вторинних хвиль безмежно вузькі. Кінцева ширина щілини буде приводити до розмивання максимумів і мінімумів. На досить широких щілинах максимуми будуть перекриватись, і інтерференція спостерігатись не буде.

Інтерференцію можна спостерігати й у білому світлі, тобто немонохроматичному світлі. У цьому випадку кожна смуга буде райдужно пофарбована, інтерференція супроводжується розкладанням світла на монохроматичні складові (чим більше значення , тим на більшій відстані перебуватимуть максимуми один від одного).

3. Інтерференція в тонких плівках. Кільця Ньютона

Не слід вважати, що інтерференцію світла можна спостерігати лише в лабораторних умовах із застосуванням спеціального обладнання. Кожному з нас не раз доводилось спостерігати за свіченням мильних плівок, олійних плям на поверхні води, кольори гартованих предметів, кольори найтонших металевих покрить фарфорових виробів, різноколірність крил різних метеликів, бджіл тощо. В усіх цих випадках інтерференція світла спостерігається в досить тонких прозорих плівках, товщина яких близька до довжини хвилі і перебуває в межах довжини когерентності.

Розглянемо плоско паралельну прозору плівку товщиною , на яку падає під кутом плоска монохроматична хвиля.

Рис. 5.

Плівка має товщину (рис. 5) і показник заломлення . Падаюча хвиля в точці А ділиться на дві частини, одна з яких 1^', змінивши фазу на протилежну, відбивається під кутом до перпендикуляра в точці падіння. Друга частина 2^' після заломлення у точці A і C відбивається в точці B. Далі промені 1^' і 2^' поширюються паралельно.

Накладання променів 1^' і 2^' здійснюється на сітківці ока спостерігача. Результати інтерференції залежать від оптичної різниці ходу цих променів.

Знайдемо оптичну різницю ходу променів 1^' і 2^', яка відповідно до рис. 5 буде дорівнювати

, (22)

де ; ; .

Підставивши значення цих величин в (22), одержимо

,

або

. (23)

Формула (23) дає залежність оптичної різниці ходу хвиль від кута заломлення і параметрів плівки.

Знайдемо залежність оптичної різниці ходу хвиль 1^' і 2^' від кута падіння , вважаючи що

і що .

Тому

,

або

. (24)

В залежності від того, яке число півхвиль вкладається в оптичній різниці ходу хвиль 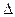плівка буде світлою (умова max), або темною (умова min).

Важливо знати:

1. При освітленні плівки білим світлом для деяких хвиль виконується умова max, а для деяких – умова min. Тому плівка буде забарвлена певним кольором.

2. Колір плівки залежить від кута падіння променя, а тому полоси інтерференції в цьому випадку називаються полосами однакового нахилу.

3. Можливість ослаблення білого світла внаслідок інтерференції широко використовується у сучасних оптичних приладах (фотоапаратах, біноклях тощо). Для цього на поверхню лінзи наносять тонкий шар прозорої плівки з показником заломлення, меншим, ніж у лінзи, і більшим, ніж у повітря. Товщину прозорої плівки беруть такою, щоб мінімуми інтерференції спостерігалися в середній частині видимого спектру ( ). Таку оптику називають просвітленою (рис.6).

Рис. 6

Промінь 1 при відбиванні від поверхні плівки змінив фазу на протилежну. Промінь 2 двічі пройшов товщину плівки і при відбиванні на нижній частині плівки теж змінив фазу на протилежну. Оптична різниця ходу в плівці буде дорівнювати

.

Якщо в 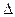вкладається непарне число півхвиль, то промені від плівки не відбиваються, тобто спостерігається умова min.

– умова min.

Окремим видом інтерференції світла є інтерференція в повітряному зазорі у вигляді клина між опуклою стороною плоско опуклої лінзи і поверхнею плоскої пластинки (рис. 7).

Рис. 7.

Промені 1 і 2 одержані з одного променя, а тому є когерентні. Оптична різниця ходу променів у повітряному зазорі дорівнює

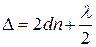, (25)

де n – показник заломлення середовища між лінзою і плоско паралельною пластинкою; – товщина зазору в указаному місці.

Промені 1 і 2 є відбитими, тому розглядається результат інтерференції у відбитому світлі. Аналогічно можна розглянути інтерференцію світла у прохідному світлі. В цьому випадку фаза поміняється на протилежну, а різниця ходу на .

Знайдемо радіуси світлих і темних кілець Ньютона у відбитому світлі.

Для світлих кілець , а для темних кілець , де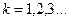

Радіус k-го кільця визначаємо з рисунка, де розглядаємо прямокутний трикутник.

, (26)

або

.

Звідки

. (27)

Для знаходження радіусів світлих кілець необхідно оптичну різницю ходу для променів у зазорі прирівняти до умови max, тобто

,

звідки

, ,

тому

. (28)

Вираз (28) дає радіуси світлих кілець Ньютона.

Для темних кілець

,

звідки

,

тому

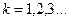, (29)

Вираз (29) визначає радіуси темних кілець Ньютона.

Важливо знати:

1. Правильна форма кілець Ньютона легко спотворюється при різних, навіть незначних, дефектах при шліфуванні різних поверхонь. Тому спостереження форми кілець Ньютона є найтоншим контролем якості шліфування поверхонь.

2. Явище інтерференції світла використовується у ряді дуже точних вимірювальних приладів, які називаються інтерферометрами. В цьому випадку точність вимірювань лінійних розмірів сягає 10^-8 мм.

3. Кільця Ньютона утворюються в зазорі між опуклою лінзою і плоско паралельною пластинкою при однаковій (різна для різних кілець) товщині зазору. Тому полоси інтерференції, якими є кільця Ньютона, носять назву полоси однакової товщини.