
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Дифракція Фраунгофера на щілині
Нехай на досить довгу вузьку прямокутну щілину шириною b перпендикулярно до неї падає плоска світлова хвиля. Розмістимо за щілиною збірну лінзу, а у фокальній площині екран для спостережень результатів дифракції (рис. 3).

Рис. 3
Щілину шириною b ділять на N вузьких смуг шириною
 (9)
(9)
де b – ширина щілини; N – число смуг на які поділено щілину; 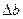 – ширина однієї смуги.
– ширина однієї смуги.
Оптична різниця ходу двох променів від однієї смуги шириною 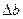 буде дорівнювати
буде дорівнювати
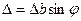 . (10)
. (10)
Оптична різниця ходу 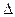 зв’язана з оптичною різницею фаз співвідношення
зв’язана з оптичною різницею фаз співвідношення
 (11)
(11)
де  – хвильове число;
– хвильове число; 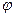 – кут дифракції .
– кут дифракції .
Для знаходження результуючої амплітуди від всіх смуг, яка буде збуджуватися в точці М (рис.3), використаємо формулу результуючої амплітуди при інтерференції багатьох хвиль
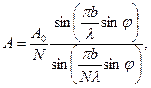 (12)
(12)
де  – амплітуда хвиль від всієї щілини; N – число смуг, на які поділена щілина шириною b;
– амплітуда хвиль від всієї щілини; N – число смуг, на які поділена щілина шириною b; 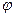 – кут дифракції.
– кут дифракції.
Розглянемо випадок, коли  . У цьому випадку
. У цьому випадку
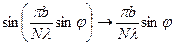 . (13)
. (13)
Формула (12) з урахуванням (13) перепишеться
 (14)
(14)
Оскільки інтенсивність світлових хвиль  пропорційна
пропорційна 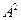 , то
, то
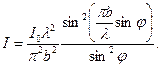 (15)
(15)
Знайдемо умови мінімуму й максимуму дифракції світлових хвиль, які приходять у точку М (рис.3) від однієї щілини. У точці М інтенсивність світлових хвиль буде дорівнювати нулю, якщо 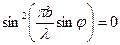 . Це можливо лише у випадку, коли
. Це можливо лише у випадку, коли  , звідки
, звідки
 (16)
(16)
де b – ширина щілини; 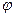 – кут дифракції; k – порядок максимуму;
– кут дифракції; k – порядок максимуму;  – довжина хвилі монохроматичного світла.
– довжина хвилі монохроматичного світла.
Умова (16) є умовою мінімуму дифракції від однієї щілини.
У точці М буде спостерігатись максимум дифракції, якщо 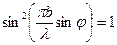 . Це можливо за умови, коли
. Це можливо за умови, коли 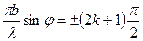 , звідки
, звідки
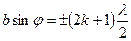 . (17)
. (17)
Умова (17) є умовою максимуму дифракції від однієї щілини.
Покажемо залежність амплітуди хвиль, які проходять від однієї щілини в точку накладання, від кута дифракції 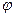 .
.
а) Якщо підставити в (12) значення кута дифракції  , то одержимо невизначеність типу
, то одержимо невизначеність типу  . Для розкривання цієї невизначеності використаємо правило Лопіталя.
. Для розкривання цієї невизначеності використаємо правило Лопіталя.
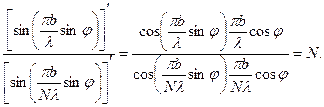 (18)
(18)
Якщо підставити цей результат в (12) одержимо
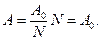 (19)
(19)
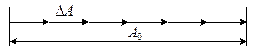
Відповідно інтенсивність хвиль буде дорівнювати
 .
.
б) Якщо 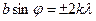 , то як уже відомо,
, то як уже відомо,  і
і  . В цьому випадку амплітуди
. В цьому випадку амплітуди 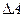 від окремих смуг, на які ми поділили щілину, після додавання дають замкнену лінію
від окремих смуг, на які ми поділили щілину, після додавання дають замкнену лінію
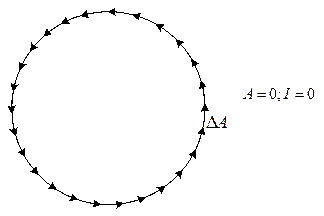
в) Якщо 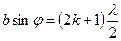 , то додавання амплітуд
, то додавання амплітуд 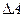 в довільній точці накладання не дає замкнутої лінії
в довільній точці накладання не дає замкнутої лінії
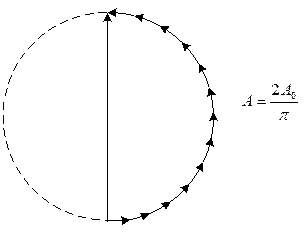
Дата добавления: 2014-12-03; просмотров: 607; Мы поможем в написании вашей работы!; Нарушение авторских прав |