Хвильові рівняння електромагнетних хвиль

Для одержання хвильових рівнянь електромагнетних хвиль, розв’язком яких є рівняння (6), скористаємось рівняннями Максвелла.

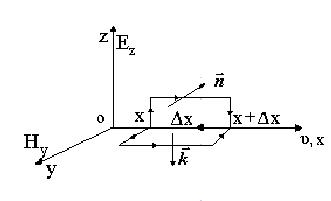
Рис. 4

Розглянемо замкнутий контур в системі координат Е_z,o,x , сторони якого відповідно дорівнюють 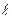і Δх. Запишемо для цього замкнутого контуру рівняння Максвелла (1)

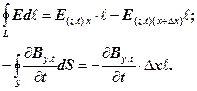
(7)

Оскільки ліві сторони рівнянь (7) відповідають рівнянню Максвелла (1), то праві сторони цих рівнянь можна прирівняти. Після незначних спрощень одержуємо

. (8)

В граничному випадку, коли 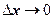рівняння (8) набуде вигляду

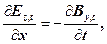
де – , зв’язок індукції магнетного поля з напруженістю цього поля. З урахуванням цього зауваження формула (8) набуде вигляду

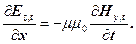(6.9)

Рівняння Максвелла (3) використаємо до замкнутого контуру в координатній площині Н_y,o,x (рис.4), вважаючи що вільні електричні заряди відсутні, а тому струм провідності jdS = 0

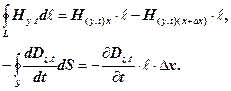(10)

Оскільки ліві сторони рівнянь (10) однакові, то й праві сторони однакові. Прирівняємо праві сторони цих рівнянь, одержимо

В граничному випадку, коли 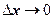, одержимо

(11)

Оскільки 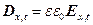, то рівняння (11) набуде вигляду

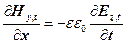. (12)

Продиференціюємо рівняння (12) по координаті х, одержимо

(13)

Замість виразу в душках правої сторони рівняння (13) підставимо його значення з рівняння (9), одержимо

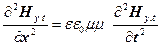. (14)

Продиференціюємо по координаті х рівняння (9)

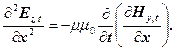(15)

Похідну в душках правої сторони рівняння (15) замінимо на відповідну похідну з рівняння (12), одержимо

(16)

З рівнянь (14) і (16) шляхом незначних перетворень одержуємо хвильові рівняння електромагнетних хвиль

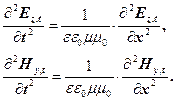(17)

Аналогічні до (17) хвильові рівняння можна одержати, якщо кожне з рівнянь (6) двічі диференціювати за часом і координатою і виключити з них функцію косинуса, тобто

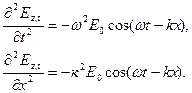
Звідки, врахувавши що , одержуємо

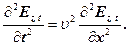(18)

Аналогічно диференціюємо друге рівняння (6) й після незначних спрощень одержуємо

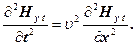(19)

Співставлення рівнянь (18) і (19) з рівняннями (17) дає можливість визначити швидкість поширення електромагнетних хвиль

(20)

Якщо врахувати, що для вакууму ε =1 і μ = 1, то швидкість поширення електромагнетних хвиль у вакуумі буде дорівнювати

(21)

Одержане значення швидкості поширення електромагнетних хвиль у вакуумі добре збігається з швидкістю поширення світла. В діелектричному середовищі (крім феромагнетиків) швидкість поширення електромагнетних хвиль менша на 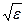, тобто

(22)

Для світлових хвиль, які можуть поширюватись в прозорих діелектричних середовищах, величину 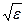називають показником заломлення і позначають через n, тому

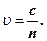(23)

3. Енергія електромагнетних хвиль. Вектор Пойнтінга

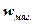Можливість виявлення електромагнетних хвиль указує на те, що вони переносять енергію. Об'ємна густина w енергії електромагнетної хвилі складається з об'ємних густин і електричного і магнетного полів:

(34)

В рівняння (9), яке дорівнює 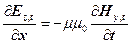підставимо необхідні похідні рівнянь (6), тобто

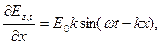
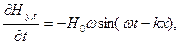
одержимо

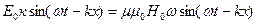. (35)

Після необхідних спрощень одержимо

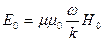. (36)

Оскільки , то вираз (36) перепишеться

. (37)

Рівність (37) справедлива не лише для амплітудних значень напруженостей електричного й магнетного полів, але й для будь-яких їх значень, тобто

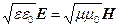. (38)

Вираз (34) густини енергії електромагнетних хвиль перепишемо в такому вигляді

,

або з урахуванням (38) одержимо

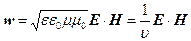. (39)

Нехай електромагнетна хвиля поширюється з швидкістю υ в напрямі осі х. Виділимо прямокутний паралелепіпед з площею торця S і стороною υΔt, як це показано на рис. 5.

Рис. 5

Повна енергія, яка буде перенесена через площадку S за час Δt буде дорівнювати

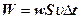. (40)

Із цієї формули знайдемо вектор потоку енергії, яка переноситься через площадку S в напрямі осі х із швидкістю υ, тобто

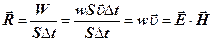. (41)

Так-як вектори Ε і Η взаємно перпендикулярні й утворять з напрямком поширення хвилі правогвинтову систему, то напрямок вектора [Е·Н] збігається з напрямком переносу енергії, а модуль цього вектора дорівнює Е·Н. Отже, вектор густини потоку електромагнетної енергії, називається вектором Пойнтінга.

Якщо електромагнетні хвилі поглинаються або відбиваються тілами, то відповідно до теорії Максвелла вони повинні здійснювати на тіла деякий тиск. Тиск електромагнетних хвиль пояснюється тим, що під дією електричного поля хвилі заряджені частинки речовини починають упорядковано рухатися і крім того з сторони магнетного поля хвилі на частинку діє сила Лоренца. Однак величина цього тиску досить мізерна. Можна оцінити, що при середній потужності сонячного випромінювання на Землю діє тиск , який не перевершує 5 мкПа. Вперше тиск електромагнетного випромінювання вдалось виміряти російському фізику Лебедєву. Поле електромагнетних хвиль має певний імпульс, величину якого можна оцінити через енергію так

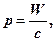(42)

де W ─ енергія електромагнетної хвилі; с ─ швидкість поширення електромагнетних хвиль.