Інтерференція багатьох хвиль

В попередніх питаннях була розглянута інтерференція лише двох когерентних хвиль. Насправді в реальних умовах інтерференція є багатохвильовою, тобто одночасно інтерферують десятки когерентних променів (рис. 8).

Рис. 8

Відбиті хвилі 1, 2, 3, 4, ..., мають спадаючу інтенсивність. В залежності від коефіцієнта відбивання інтенсивність цих хвиль може відрізнятись у сотні разів. Аналогічні властивості мають прохідні промені 1^', 2^', 3^', 4^', ... .

Амплітуди відбитих хвиль досить різко відрізняються між собою

Промені 1,2,3,4,5,6, ... (рис. 8) зсунуті по фазі на однакову величину . Це пов’язано з тим, що оптична різниця ходу сусідніх променів є сталою величиною.

Для спрощення розглянемо випадок, коли відбиті плоскі хвилі мають однакову амплітуду A₀ і сталу різницю фаз . Результуючу амплітуду при інтерференції N хвиль легко визначити, скориставшись векторною діаграмою. Кожна хвиля в цьому випадку зсунута по фазі по відношенню до попередньої хвилі на сталу величину (рис. 9).

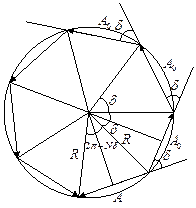
Рис. 9.

З рисунка видно, що

. (30)

З трикутника, який розміщений рядом

. (31)

Але

. (32)

Поділивши (30) на (31) та врахувавши вираз (32), одержимо

. (33)

Вираз (33) дає можливість розрахувати результуючу амплітуду при накладанні багатьох хвиль, зсунутих по фазі на сталу величину .

Інтенсивність хвиль у цьому випадку пропорційна квадрату амплітуди, тобто

. (34)

Проведемо короткий аналіз виразів (33) і (34).

1. Нехай , де , тоді , одержуємо невизначеність .

Для розкривання невизначеності скористаємось правилом Лопіталя

.

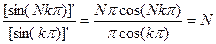У цьому випадку 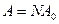, а . Графічна інтерпретація цих результатів така (рис. 10):

Рис.10.

Одержані головні максимуми інтерференції.

2. Нехай , де , тоді

і .

Для будь-яких значень k одержуємо, що 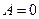і . Одержані головні мінімуми інтерференції. До уваги не беруться , , і т.д., так як там розміщуються головні максимуми.

Графічна інтерпретація цього результату така:

3. Нехай , де

У цьому випадку будуть отримані побічні максимуми.