Вынужденные колебания. Резонанс

Вынужденными колебаниями называются колебания, возни­кающие в системе при участии внешней силы, изменяющейся по периодическому закону.

Предположим, что на материальную точку, кроме квазиупру­гой силы и силы трения, действует внешняя вынуждающая сила

где F₀ — амплитуда, — круговая частота колебаний вынуждаю­щей силы. Составим дифференциальное уравнение (второй закон Ньютона):

или

(5.41)

Решение дифференциального уравнения (5.41) является сум­мой двух слагаемых. Одно из них, соответствующее уравнению затухающих колебаний (5.20), играет роль только при установле­нии колебаний (см. рис. 5.6). Со временем им можно пренебречь. Другое слагаемое описывает смещение материальной точки в ус­тановившихся вынужденных колебаниях

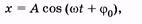(5.42)

где

(5.43)

(5.44)

Как видно из (5.42), установившееся вынужденное колебание, происходящее под воздействием гармонически изменяющейся вы­нуждающей силы, тоже является гармоническим. Частота вынуж­денного колебания равна частоте вынуждающей силы. Вынужден­ные колебания, график которых представлен на рис. 5.17, сдвину­ты по фазе относительно вынуждающей силы.

Амплитуда вынужденного колебания (5.43) прямо пропорци­ональна амплитуде вынуждающей силы и имеет сложную зави­симость от коэффициента затухания среды и круговых частот соб­ственного и вынужденного колебаний. Если w₀ и b для системы заданы, то амплитуда вынужденных колебаний имеет максималь­ное значение при некоторой определенной частоте вынуждающей силы, называемой резонансной. Само явление — достижение максимальной амплитуды вынужденных колебаний для за­данных w₀ и b — называют резонансом.

Резонансную круговую частоту можно найти из условия мини­мума знаменателя в (5.43):

(5.45)

Подставив (5.45) в (5.43), находим амплитуду при резонансе:

(5.46)

Из (5.46) видно, что при отсутствии сопротивления амплитуда вынужденных колебаний при резонансе неограниченно возрастает. При этом из (5.45) следует, что , т. е. резонанс в системе без затухания наступает тогда, когда частота вынуж­дающей силы совпадает с частотой собственных колебаний. Гра­фическая зависимость амплитуды вынужденных колебаний от круговой частоты вынуждающей силы при разных значениях ко­эффициента затухания показана на рис. 5.18.

Механический резонанс может быть как полезным, так и вред­ным явлением. Вредное действие резонанса связано главным об­разом с разрушением, которое он может вызвать. Так, в технике, учитывая разные вибрации, необходимо предусматривать воз­можное возникновение резонансных условий, в противном случае могут быть разрушения и катастрофы. Тела обычно имеют не­сколько собственных частот колебаний и соответственно несколь­ко резонансных частот.

Если бы коэффициент затухания внутренних органов человека был невелик, то резонансные явления, возникшие в этих органах под воздействием внешних вибраций или звуковых волн, могли бы привести к трагическим последствиям: разрыву органов, по­вреждению связок и т. п. Однако такие явления при умеренных внешних воздействиях практически не наблюдаются, так как ко­эффициент затухания биологических систем достаточно велик. Тем не менее резонансные явления при действии внешних меха­нических колебаний происходят во внутренних органах. В этом, видимо, одна из причин отрицательного воздействия инфразвуковых колебаний и вибраций на организм человека (см. § 6.7 и 6.8).