КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Уравнение механической волны
Механической волной называют механические возмущения, распространяющиеся в пространстве и несущие энергию.
Различают два основных вида механических волн: упругие волны (распространение упругих деформаций) и волны на поверхности жидкости.
Упругие волны возникают благодаря связям, существующим между частицами среды: перемещение одной частицы от положения равновесия приводит к перемещению соседних частиц. Этот процесс распространяется в пространстве с конечной скоростью.
Уравнение волны выражает зависимость смещения колеблющейся точки (s), участвующей в волновом процессе, от координаты ее равновесного положения и времени. Для волны, распространяющейся вдоль направления ОХ, эта зависимость записывается в общем виде:
Если s и х направлены вдоль одной прямой, то волна продольная, если они взаимно перпендикулярны, то волна поперечная.
Выведем уравнение плоской волны. Пусть волна распространяется вдоль оси ОХ (рис. 5.20) без затухания так, что амплитуды колебаний всех точек одинаковы и равны А. Зададим колебание точки с координатой х = 0 (источник колебаний) уравнением
До точки с некоторой произвольной координатой х возмущение от начала координат дойдет через время t, поэтому колебания этой точки запаздывают:
(5.47)
Так как время и скорость распространения волны связаны зависимостью 
то вместо (5.47) получаем
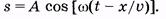(5.48)
Это и есть уравнение плоской волны, которое позволяет определить смещение любой точки, участвующей в волновом процессе, в любой момент времени. Аргумент при косинусе j= w(t - x/u) называют фазой волны. Множество точек, имеющих одновременно одинаковую фазу, называют фронтом волны. Для рассмотренного случая фронтом волны будет плоскость х = const (плоскость, перпендикулярная оси ОХ), всем точкам которой соответствует одновременно одинаковая фаза. Отсюда и название — плоская волна.
Скорость распространения фиксированной фазы колебаний называют фазовой. Предположим, что 
Продифференцировав это равенство, получим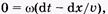 
откуда 
Следовательно, скорость распространения фиксированной фазы колебаний и есть скорость распространения волны.
Кроме фазовой скорости различают еще групповую скорость, которую вводят тогда, когда реальная волна не может быть представлена одним гармоническим уравнением (5.48), а является суммой группы синусоидальных волн.
Длиной волны называют расстояние между двумя точками, фазы которых в один и тот же момент времени отличаются на 2p. Онаравна расстоянию, пройденному волной за период колебания:
(5.49)
Уравнение волны (5.48) — одно из возможных решений общего дифференциального уравнения с частными производными, описывающего процесс распространения возмущения в среде. Такое уравнение называют волновым. Чтобы иметь представление о волновом уравнении, продифференцируем (5.48) дважды по времени t и дважды по координате х:.
(5.50)
(5.51)
Сравнивая вторые производные в (5.50) и (5.51), получаем одномерное волновое уравнение
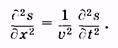(5.52)
Решение уравнений с частными производными выходит за пределы данного курса. Одно из решений (5.48) известно. Однако важно отметить следующее. Если изменение какой-либо физической величины: механической, тепловой, электрической, магнитной и т. д. — отвечает уравнению (5.52), то это означает, что соответствующая физическая величина распространяется в виде волны со скоростью u.
Дата добавления: 2014-10-31; просмотров: 595; Мы поможем в написании вашей работы!; Нарушение авторских прав |