Одновимірне хвильове рівняння. Швидкість поширення хвиль

Рівняння довільної хвилі є розв'язком рівняння, яке називається хвильовим.

Для виведення цього рівняння скористаємось рівняння плоскої хвилі, яка поширюється в напрямку осі х. Розглянемо ділянку пружного середовища, яке характеризується модулем пружності Е (рис. 2). З рисунка видно, що виділений елемент має переріз S і довжину Δх. Під дією зовнішньої сили F виділена ділянка пружного середовища деформується на величину ΔU.

Рис. 2

Оскільки середовище є пружним, то для виділеної ділянки можна застосувати закон Гука

(8)

де Е – модуль Юнга;

– відносна деформація;

F – зовнішня сила;

S – площа виділеної ділянки пружного середовища в напрямі осі х.

В граничному випадку при , рівняння (8) запишеться так

(9)

Якщо збуджувати поздовжню хвилю в деякому пружному середовищі, яким є наприклад стержень перерізом S з модулем Юнга Е, то на виділену ділянку будуть діяти дві сили (рис.3). Запишемо для цієї ділянки другий закон Ньютона

(10)

Сили в рівнянні (10) є пружними силами, а тому відповідно до рівняння (9) запишуться так

(11)

Якщо підставити ці сили (11) в другий закон Ньютона (10), то після деяких перетворень одержимо

(12)

де m ─ маса виділеної ділянки пружного середовища.

Масу виділеної ділянки пружного середовища можна виразити через об’єм і густину речовини стержня так

m = ρSΔx. (13)

Рис.3

З урахуванням значення маси (13) і нескладних перетворень рівняння (12) запишеться так

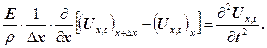(14)

Розглянувши граничний випадок при якому , з рівняння (14) одержуємо рівняння, яке називається хвильовим рівнянням

(15)

Рівняння (15) є лінійним диференціальним рівнянням другого порядку в частинних змінних. Розв’язком такого рівняння є уже відоме рівняння плоскої хвилі

(16)

Знайдемо другі частинні похідні за часом t і координатою х від рівняння (16)

(17)

Після підстановки відповідних похідних (17) в рівняння (15) та необхідних скорочень одержимо

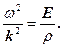(18)

Але оскільки , то хвильове рівняння (15) буде мати інший вигляд

(19)

Таким чином швидкість поширення механічних хвиль у пружному середовищі залежить від пружних властивостей цього середовища і його густини

(20)

Оскільки модуль Юнга характеризує стиснення або розтяг пружного середовища, то одержана швидкість (20) є фазовою швидкістю лише поздовжніх хвиль.

Фазова швидкість поперечних хвиль, які можуть існувати лише в твердому пружному середовищі, визначають заміною модуля Юнга в (20) на модуль зсуву G

(21)

Розрахунки показують, що в твердому середовищі модуль Юнга E майже на порядок перевищує величину модуля зсуву G, тому фазова швидкість поздовжньої хвилі тут більша за швидкість поперечної хвилі, тобто

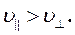(22)

Важливо відмітити, що для механічних хвиль, які мають велику довжину λ рівняння (15) і (19) будуть нелінійними.

Якщо механічна хвиля поширюється в однорідному ізотропному середовищі, то хвильове рівнянням буде мати вигляд:

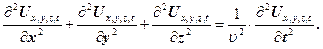(23)

Для механічних хвиль властивий принцип суперпозиції. Це означає, що при накладанні механічних хвиль відсутнє їх спотворення.