Дифракція світла. Принцип Гюйгенса - Френеля. Метод зон Френеля

6.5.1. Дифракція світла – це сукупність явищ, які зумовлені хвильовою природою світла і спостерігаються в середовищах з різкими неоднорідностями (наприклад, при проходженні світла через отвори, поблизу границь непрозорих тіл і т.п.). Дифракція, зокрема, приводить до огинання світловими хвилями перешкод і проникання світла в область геометричної тіні. Для спостереження дифракції необхідно, щоб розміри перешкод були співмірні з довжиною хвилі світла.

Проникнення світла в область геометричної тіні пояснює принцип Гюйгенса: кожна точка фронту хвилі є джерелом вторинної сферичної хвилі; положення фронту хвилі в наступний момент визначається огинаючою фронтів усіх вторинних хвиль. Принцип Гюйгенса не дозволяє знайти інтенсивність дифрагованої хвилі. Цей недолік усунув Френель, який доповнив принцип Гюйгенса уявленням про інтерференцію вторинних хвиль.

Нехай S (рис.6.13) – хвильова поверхня світла, яке поширюється від деякого джерела. Кожен елемент поверхні служить джерелом вторинної хвилі. При цьому вважатиметься, що вторинні хвилі від усіх елементів – когерентні. Від кожного елемента поверхні dS в точку Р приходить коливання

(6.24)

Тут – амплітуда і фаза коливання в місці знаходження хвильової поверхні S, k – хвильове число, r – відстань від елемента dS до точки Р. Коефіцієнт залежить від орієнтації елемента dS відносно r. Результуюче коливання в точці Р, згідно з Френелем, є суперпозицією коливань усієї хвильової поверхні S:

. (6.25)

Формула (6.25) є аналітичним виразом принципу Гюйгенса-Френеля.

6.5.2. В ряді дифракційних задач, що мають осьову симетрію, розрахунок інтерференції вторинних хвиль спрощується за допомогою розбиття фронту хвилі на кільцеві зони Френеля. Розбиття на зони проводиться таким чином, що оптична різниця ходу від відповідних точок кожної пари сусідніх зон до точки спостереження Р дорівнює . Вторинні хвилі від відповідних точок двох сусідніх зон приходять в точку Р у протифазі і послаблюють одна одну при накладанні (рис.6.14).

Нехай – величини результуючих амплітуд хвиль, які приходять в точку Р від кожної зони. Сумарна амплітуда в точці Р від усього фронту буде дорівнювати

(6.26)

де відповідає непарному числу зон, а знак “–” – парному.

За рахунок збільшення кута нахилу j з ростом номера зони і відстані до точки Р, амплітуди хвиль монотонно зменшуються Можна вважати, що

(6.27)

Тепер результуючу амплітуду А можна записати у вигляді

Очевидно, що вирази в дужках дорівнюють практично нулю; тоді

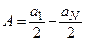(6.28)

для парного числа зон Френеля. Результуюча амплітуда при цьому мінімальна, і в точці Р буде мінімум освітленості. Якщо ж N – непарне, то

, (6.29)

і в точці Р спостерігається максимум освітленості. Для повністю відкритої хвильової поверхні і , тому 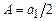, тобто дія всієї хвильової поверхні еквівалентна дії половини центральної зони Френеля.

Якщо дифракція світла відбувається на круглому непрозорому диску, який закриває N перших зон Френеля, то результуюча амплітуда в точці Р буде визначатися величиною

. (6.30)

Дифракційна картина у цьому випадку має вигляд концентричних світлих і темних кілець. В центрі картини при довільному N (парному чи непарному) спостерігається світла пляма (пляма Пуасона). При збільшенні розмірів диску величина амплітуди буде зменшуватись. Врешті-решт при досить великих розмірах диску і . При цьому в точці Р буде темна пляма – геометрична тінь.

Таким чином, закони геометричної оптики можна застосовувати у тих випадках, коли розміри перешкод і отворів великі порівняно з довжиною хвилі світла.