Елементи геометричної оптики: закони відбивання і заломлення світла; тонкі лінзи

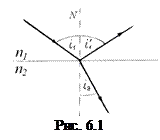6.1.1. В основі геометричної оптики лежать закони відбивання і заломлення світла. Закон відбивання твердить, що відбитий промінь лежить в одній площині з падаючим променем і нормаллю N, проведеною в точці падіння; при цьому кут відбивання дорівнює куту падіння 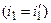. Закон заломлення: промінь падаючий, заломлений і нормаль в точці падіння лежать в одній площині; відношення синуса кута падіння до синуса кута заломлення є величина стала для даної пари двох середовищ і рівна відносному показнику заломлення другого середовища відносно першого (рис.6.1):

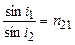_. (6.1)

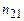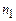Відносний показник заломлення – це відношення абсолютних показників заломлення середовищ і , де 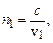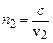(с – швидкість світла у вакуумі, і 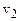– швидкості світла в першому і другому середовищах).

Отже,

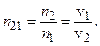(6.2)

Якщо промінь поширюється з оптично більш густого середовища в менш густе , то при деякому граничному куті падіння заломлений промінь буде ковзати вздовж межі поділу двох середовищ, тобто 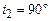. При куті падіння 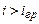світловий промінь повністю відбивається. В цьому полягає суть явища повного внутрішнього відбивання (рис.6.2). Очевидно, в цьому випадку

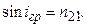(6.3)

На явищі повного внутрішнього відбивання базується робота приладів (рефрактометрів), які дозволяють визначати показник заломлення середовища.

6.1.2.Лінза називається тонкою, якщо її товщина d мала порівняно з радіусами кривизни її поверхонь і 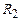(рис. 6.3). Головною оптичною віссю лінзи називають пряму, що проходить через центри кривизни її поверхонь. Можна вважати, що в такій лінзі точки перетину головної оптичної осі з обома поверхнями лінзи співпадають. Цю точку називають центром лінзи. Промені, які проходять через центр лінзи, не зазнають заломлень.

Величину

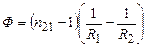(6.4)

називають оптичною силою тонкої лінзи і 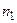– абсолютні показники заломлення матеріалу лінзи і оточуючого середовища). Для збірної (додатної) лінзи Ф>0, для розсівної (від’ємної) Ф<0. Точки, що лежать на головній оптичній осі лінзи по обидві сторони від оптичного центру на відстанях f, 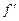, називають головними фокусами лінзи (рис. 6.4): .

Для першого головного фокуса F

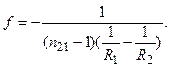(6.5)

Аналогічно, друга головна фокусна відстань

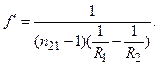(6.6)

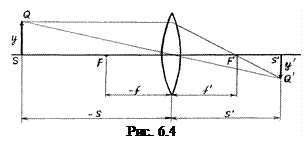Площини, які проходять через головні фокуси F і 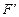лінзи перпендикулярно до головної оптичної осі, називаються фокальними площинами лінзи.

Найчастіше буває, що речовина по обидва боки від лінзи одна й та ж (наприклад, повітря). Тоді головні фокусні відстані чисельно дорівнюють одна одній. Протилежні знаки означають, що головні фокуси лежать з різних боків від лінзи. Для збірної лінзи (оскільки Ф>0) , для розсівної лінзи (оскільки Ф<0)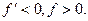

Для лінз справедливе основне рівняння

, (6.7)

де всі відрізки відраховуються від центру лінзи, а радіуси кривизни завжди напрямлені від вершини поверхні до центру її кривизни. Вони вважаються додатними, якщо напрямлені в сторону поширення світла. Відрізки, перпендикулярні до оптичної осі, відраховуються від оптичної осі; вони додатні вище оптичної осі і від’ємні нижче оптичної осі.

При розв’язуванні задач основне рівняння тонкої лінзи (6.7) записують у вигляді

, (6.8)

де 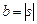, , 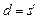знак плюс відповідає збірній лінзі, знак мінус – розсівній.

Лінійне збільшення тонкої лінзи визначається як

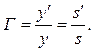(6.9)

Для дійсних зображень Г < 0, тобто вони обернені; для уявних зображень Г>0, тобто вони прямі.

Оптична сила Ф центрованої системи двох тонких лінз з оптичними силами Ф₁ і Ф₂ на відстані d одна від одної дорівнює

(6.10)