Електромагнітні коливання

Електромагнітними коливаннями називаються процеси, при яких періодично змінюються з часом характеристики електричних і магнітних полів (заряд, сила струму, напруженість поля тощо). Джерелом електромагнітних коливань може бути коливальний контур, який складається з конденсатора ємністю С, котушки з індуктивністю L та резистора з опором R (рис. 5.12).

Нехай у початковий момент часу конденсатор зарядили до різниці потенціалів U, після чого джерело від’єднали. Тоді по колу піде зростаючий розрядний струм. Коли потенціали обкладок конденсатора вирівняються, а в котушці індуктивності струм досягне максимального значення, е.р.с. самоіндукції в котушці підтримає спадаючий струм і відбудеться перезарядка конденсатора. Після цього знову виникне струм, але протилежного напрямку. Оскільки перезарядка конденсатора буде відбуватися періодично, то в контурі виникнуть електромагнітні коливання.

Такі коливання подібні до механічних, наприклад, до коливань маятника. Відхилений маятник за інерцією проходитиме положення рівноваги, відхиляючись у протилежну сторону, і продовжуватиме коливальний рух. Із такого порівняння видно, що індуктивність контура відіграє роль інерції, а опір – роль сил тертя.

За ІІ правилом Кірхгофа алгебраїчна сума спадів напруг на ділянках контура рівна алгебраїчній сумі електрорушійних сил, що зустрічаються у контурі:

. (5.73)

Оскільки , а , то (5.73) можна переписати як

або

,

чи

. (5.74)

Ввівши позначення

,

отримаємо диференціальне рівняння коливань заряду на пластинах конденсатора

,

де – власна циклічна частота коливань, b – коефіцієнт згасання.

За аналогією з механічними коливаннями розв’язок цього рівняння має вигляд

, (5.75)

де циклічна частота згасаючих коливань рівна

або

.

Величина

є амплітудою згасаючих коливань. Використавши (5.75), можна встановити вирази для коливань напруги на конденсаторі 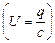і сили струму в контурі . Період електромагнітних згасаючих коливань

.

Якщо опір (ідеальний контур), то в контурі встановляться незгасаючі коливання величин з періодом

. (5.76)

Вираз (5.76) називають формулою Томсона для гармонічних електромагнітних коливань. Відмітимо, що коливання струму зміщені в ідеальному контурі по фазі на p порівняно з коливанням заряду і напруги, оскільки .