Хвильове рівняння

Хвильове рівняння – це диференціальне рівняння, розв’язком якого є рівняння хвилі. Для встановлення хвильового рівняння співставимо другі частинні похідні по координатах і часу від рівняння хвилі (5.50)

.

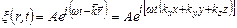Тоді:

, (5.51)

(5.52)

Просумуємо систему рівнянь (5.52):

. (5.53)

Співставляючи (5.51) і (5.53), одержимо

. (5.54)

Оскільки

, (5.55)

то остаточно хвильове рівняння набуває вигляду

. (5.56)

Ліву частину цього рівняння можна лаконічно записати, використовуючи позначення оператора Лапласа як суму других частинних похідних по х, у, z від функції цих змінних. Тоді хвильове рівняння матиме вигляд

.

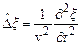Для плоскої хвилі, що поширюється вздовж осі х, хвильове рівняння набуде вигляду

. (5.57)

Поширення коливань у пружному середовищі зумовлене поширенням деформації середовища під дією джерела хвилі. І тому швидкість поширення хвилі повинна визначатись пружними характеристиками середовища.

Зокрема, швидкість поздовжніх хвиль в твердих тілах

, (5.58)

в рідинах і газах

, (5.59)

де Е – модуль Юнга, k – модуль всебічного стиску.

Швидкість поперечних хвиль в твердих тілах

де G – модуль зсуву.

Швидкість звуку в газах

де 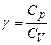– відношення молярних чи питомих теплоємностей при сталих тиску та об’єму, 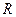– універсальна газова постійна, Т – термодинамічна температура, μ – молярна маса газу.