
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Згасаючі коливання
Реальні коливання відбуваються в умовах дії сил тертя (опору). І тому реальні коливні системи є дисипативними, в яких механічна енергія частково втрачається, що призводить до поступового зменшення амплітуди, тобто до згасання коливань. Для спрощення обмежимось випадком лінійного коливання матеріальної точки у в’язкому середовищі. Якщо швидкість коливального руху невелика, то сила опору пропорційна до швидкості і напрямлена проти швидкості, тобто
 ,
,
де r – коефіцієнт опору.
Тоді за другим законом Ньютона
 . (5.27)
. (5.27)
Розділивши рівність (5.27) на m, отримаємо
 . (5.28)
. (5.28)
Введемо позначення
 .
.
Рівняння (5.28) матиме вигляд диференціального рівняння згасаючих коливань:
 . (5.29)
. (5.29)
Підстановкою
 (5.30)
(5.30)
приведемо рівняння (5.29) до простішого вигляду (тут е – основа натурального логарифму). Заміну змінних у (5.29) проведемо за допомогою рівнянь
 (5.31)
(5.31)
Підставляючи (5.30) і (5.31) у (5.29), отримаємо

або
 . (5.32)
. (5.32)
У випадку, коли  , можна ввести заміну
, можна ввести заміну  Тоді рівняння (5.32) прийме вигляд
Тоді рівняння (5.32) прийме вигляд
 (5.33)
(5.33)
розв’язком якого є
 . (5.34)
. (5.34)
У випадку, коли  , рух матеріальної точки буде неперіодичним (аперіодичним).
, рух матеріальної точки буде неперіодичним (аперіодичним).
Підставляючи (5.34) у (5.30), одержимо рівняння руху коливної точки під дією квазіпружної сили та сили опору, тобто рівняння згасаючих коливань:
 . (5.35)
. (5.35)
З (5.35) видно, що амплітуда коливань зменшується з часом за експоненціальним законом (рис. 5.6):

 . (5.36)
. (5.36)
Фізично β характеризує швидкість зменшення амплітуди і називається коефіцієнтом згасання. Можна показати, що β чисельно дорівнює оберненій величині часу τ, протягом якого амплітуда зменшується в е раз. Дійсно, якщо  , то із (5.36) слідує, що
, то із (5.36) слідує, що

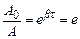 .
.
Звідси
 .
.
Зручно користуватись поняттям логарифмічного декременту згасання λ, як натурального логарифму відношення двох послідовних амплітуд (через період Т):
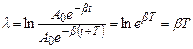 .
.
Дата добавления: 2014-12-03; просмотров: 445; Мы поможем в написании вашей работы!; Нарушение авторских прав |