Моделі систем керування з ШІМ-І.

При імпульсній модуляції першого роду величина модульованого параметра (часове положення імпульсу управління на періоді роботи перетворювача) визначається вихідним керуючим сигналом , обчисленим або виміряним в заздалегідь задані фіксовані моменти часу. Рівняння для визначення параметра, що модулюється має вигляд

. (4)

З розв’язку рівняння (3.1) визначається один або декілька коренів ; де фіксований момент часу, .

Рівняння виду (4) можуть вирішуватися відносно параметра, що модулюється, як явно, так і бути трансцендентними. Загальним виглядом математичної моделі ШІМ-І, яка дає можливість обчислити модульований параметр в явному вигляді, є поліноміальна модель

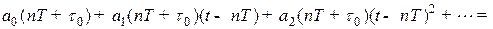
(5)

Поліноміальні коефіцієнти визначаються в задані моменти значенням сигналу . Вибір модульованого параметра може відповідати як мінімальному кореню рівняння (5), так і іншим кореням.

На практиці найбільш широке поширення знайшли рівняння виду (5) першого ступеня. Можливі варіанти реалізації ШІМ–І, що описуються рівнянням першого ступеня (5), наведені в табл. 1.

Таблиця 1.

Номер по порядку	Часова діаграма ШІМ-І	Рівняння ШІМ-І
		;

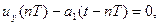
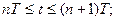
Cтруктурна схема реалізації ШІМ–І, що відповідає, п.4. табл.1, наведена на рис. 3.

Рис.3. Структурна схема реалізації ШІМ-І

В моменти часу система пам’яті (СП) запам’ятовує значення напруги . Напруга величиною потрапляє на неінвертуючий вхід (1) компаратора (К), а на інший вхід (2) потрапляє напруга з генератора пилоподібної напруги (ГПН). Так як кут нахилу напруги ГПН відомий, то значення однозначно визначає величину , що видно з побудови трикутника ( ) п.4., табл.1. Подібні схемні рішення використовуються й до інших способів формування величини наведених в табл.1.

Як опорні функції можуть використовуватись синусоїдні та експоненціальні функції. Наприклад, якщо тривалість імпульсу визначається з умови виконання рівності між постійною функцією та деякою синусоїдальною функцією, початкова фаза якої залежить від напруги , наведеною на рис. 4 а, тобто:

то підставивши допоміжну опорну напругу  і визначивши з виразу отримуємо, що:

або .

а) при синусоїдальній опорній напрузі; б) при експоненційній опорній напрузі.

Рис. 4. Діаграми формування відліку часового положення імпульсів керування

При використанні експоненціальних функцій для визначення модульованого параметра необхідно вирішувати трансцендентні рівняння. Наприклад, якщо тривалість модульованого параметра визначається порівнянням опорної функції

з функцією

то модульований параметр визначається з розв’язку трансцендентного рівняння (рис. 4,б)

.

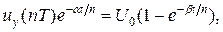
При реалізації багатоканального способу регулювання інтервал, на якому визначається модульований параметр знаходиться з виразу

де число каналів формування імпульсів управління, номер каналу.

Крім однократної ШІМ, при якій модульований параметр визначався одним з коренів рівняння (5), на практиці часто зустрічається багатократна імпульсна модуляція, при якій модульований параметр на періоді проходження вихідної напруги (струму) перетворювача визначається декількома або всіма коренями рівняння (4).

Наприклад, при формуванні синусоїдальної вихідної напруги перетворювача за допомогою ШІМ-І (рис.3.3) необхідно визначити всі корені рівняння вигляду , ( число інтервалів пилоподібної напруги, що складають період Т вихідної напруги).

Рис. 5. Формування часового положення імпульсів керування

за синусоїдальною напругою

Якщо приймати період (рис.5) як основний, то при такому підході модуляція, що розглядається зводиться до раніше показаної і більш простої модуляції (див. табл. 1, п.5). Тому в залежності від вибраного періоду, відносно якого визначається корінь рівняння (4) і число імпульсів управління, що формуються на цьому періоді, визначають або один, або декілька, або всі корені рівняння (4).

Таким чином, математична модель ШІМ-І зводиться до опису деякою функцією опорного сигналу опису сигналу, один з параметрів якого є функцією сигналу управління обчисленому в заздалегідь відомий фіксований момент часу та визначення одного або декількох вибраних з коренів рівняння вигляду (4). Знайдений корінь визначає величину модульованого параметра на му періоді роботи перетворювача.