Відкриті резонатори.

Це резонатори на основі відкритих ліній передач. Вони мають електромагнітний контакт з відкритим простором. Звичайно використовуються в лазерах сферичні діелектричні резонатори. Нас цікавлять шари діелектрика для лінії 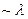. Тут не можна використовувати геометричні наближення, потрібно розв’язувати рівняння Максвела.

Розв’яжемо рівняння Максвела для сферичного діелектричного резонатора. Тут потрібно використати ССК:

, .

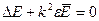В сферичній СК не можна перейти до скалярних рівнянь звичайним чином. Використовують заміну: , , , , , .

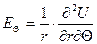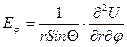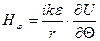Це – ТМ чи Е – заміна, оскільки . Аналогічно можна зробити Н – заміну:

Ми будемо використовувати Е – заміну, перейшовши до потенціалу , в результаті одержимо: .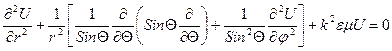

Щоб отримати саме хвильове рівняння, де була б ще й похідна 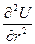, необхідно зробити заміну: . Потенціали 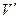та називають потенціалами Дебаю. Вони мають методичне значення. Розв’яжемо простіше рівняння для та - методом відокремлених змінних: тоді .

Рівняння для - це рівняння Лежандра. Його розв’язки – поліноми Лежандра. Рівняння для 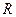можна звести до рівняння Бесселя заміною 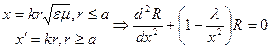. Це рівняння для сферичних функцій Бесселя (або функцій Бесселя напівцілого вигляду). Стандартний вигляд рівняння: 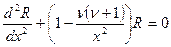, його розв’язки :

.

Таким чином розв’язки:

.

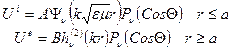Щоб використати граничні умови, необхідно виразити , 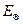через .

,

отримаємо два рівняння для А та В, причому А і В будуть відмінні від нуля лише тоді, коли системи рівна нулю. Користуючись виразами для та 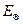, отримаємо: 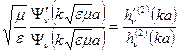з цього рівняння отримаємо . Для 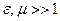: . Поле має вигляд:

Таким чином, поля тут ідуть таким же чином, як і в кільці, по якому біжить струм.

Це була строга, точна теорія резонаторів сферичної форми. Проте, їх важко виготовляти, вони незручні у використанні. Використовують:

Розрахувати таку систему неможливо, бо немає регулярних граничних умов (наприклад при ).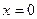

Можна вважати, що резонансна частота є проміжним значенням між резонансною частотою у вписаній та описаній кулі.

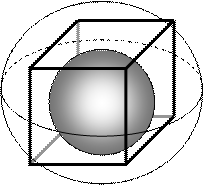Відмінність формування граничних умов:

- регулярна гранична умова

- нерегулярна гранична умова

Коли є металева поверхня, можна записати 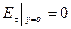. Це так звані електричні стінки.