Малюнок № 6.3.

Наведемо без виведення ряд рівнянь прямої, які будуть потрібні при розв’язуванні задач (див. таблицю № 6.1.).

	рівняння пучка прямих, що проходять через точку М0(х0;у0).
	рівняння прямої, яка проходить через дві дані точки М1(х1;у1) та М2(х2;у2).
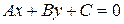
	Загальне рівняння прямої.

Таблиця № 6.1. Види рівнянь прямої.

Виведемо формулу кута між двома прямими y=k₁x+b₁ і y=k₂x+b₂ (див. малюнок № 6.4.). Для цього пригадаємо, що кутовий коефіцієнт це тангенс кута нахилу прямої до осі абсцис. Із трикутника МНК видно, що , бо зовнішній кут трикутника МНК. Звідси . Отже, маємо: 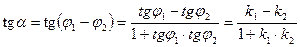. Ця формула дозволяє знаходити кут між двома прямими, які задані своїми рівняннями з кутовими коефіцієнтами.

Якщо в загальному рівнянні прямої визначити у, то при В≠0 загальне рівняння прямої приймає вигляд . Якщо позначити - через , а через 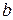, то рівняння приймає вигляд , тобто матиме вигляд рівняння прямої з кутовим коефіцієнтом. Якщо , то рівняння буде мати вигляд Ах+С=0 або х=а, тобто має рівняння прямої, паралельної осі ординат. Якщо А=0, то маємо рівняння Вх+С=0 або у=b, тобто рівняння прямої, паралельної осі абсцис.