
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Розв’язання. У системі координат будуємо графіки двох функцій: у1=х і у2=│х│
У системі координат будуємо графіки двох функцій: у1=х і у2=│х│. Після цього слід відповідно до означення додати відповідні ординати. Щоб це було легше зробити, використаємо означення модуля. Отже, розглянемо два випадки: 1) х≥0; 2) х<0. У першому випадку у1+у2=х+х=2х. Це означає, що на проміжку [0;+∞) графіком суми функцій буде пряма у=2х. Якщо х<0, то у1+у2=х+(-х)=х-х=0. Це означає, що на проміжку (-∞;0) графіком суми функцій буде пряма у=0. Як відомо, це вісь абсцис. Таким чином, графік функції у=х+│х│ складається з двох променів із спільним початком в точці з координатами О(0;0). Міркуючи аналогічно, можна прийти до висновку, що графік функції у=х•│х│ також складатиметься з двох частин: при х≥0 маємо у1•у2=х•х=х²; при х<0 будемо мати у1•у2=х•(-х)= -х². Таким чином, при х≥0 графіком функції у=х•│х│ буде вітка параболи у=х², а при х<0 – вітка параболи у=-х². Пропонуємо студентам виконати відповідні побудови самостійно.
Цілком зрозуміло, що будувати графіки саме таким способом не завжди зручно. Саме тому в математиці сформульовані та доведені твердження, які надають можливість значно спростити відшукання відповіді на запитання: що ж будує графіком функції? Наприклад, як побудувати графік функції у=Af(ax+b)+B, де A, B, a, b – сталі, причому А≠0 і а≠0. Щоб дати відповідь на це запитання сформулюємо і приймемо без доведення наступні леми та наслідки з них.
Лема 1: графік функції g(x), що визначається рівністю g(x)=f(x-α)+β, де (x-α)єD(f), а α і β – сталі, утворюється з графіка функції f паралельним перенесенням, при якому початок координат О(0;0) переходить в точку О′(α;β).
Звернемо увагу на те, що при практичному використанні леми 1 діють інакше: через точку О′(α;β) проводять допоміжні осі координат О′х′ і О′у′. У системі координат х′О′у′ будують графік у′=f(х′). Цей графік відносно системи координат хОу і є графіком функції g(x)=f(x-α)+β.
Лема 2: графік функції  , де
, де  , а
, а 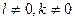 - сталі, утворюється з графіка функції f розтягом від осі абсцис з коефіцієнтом
- сталі, утворюється з графіка функції f розтягом від осі абсцис з коефіцієнтом 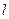 і наступним розтягом від осі ординат з коефіцієнтом k.
і наступним розтягом від осі ординат з коефіцієнтом k.
Із лем 1 і 2 випливають наступні наслідки.
Наслідок 1: графік функції g, що визначається рівністю  де
де  , утворюється з графіка функції f перетворенням симетрії відносно осі абсцис.
, утворюється з графіка функції f перетворенням симетрії відносно осі абсцис.
Наслідок 2: графік функції g, що визначається рівністю 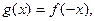 дн
дн 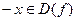 , утворюється з графіка функції f перетворенням симетрії відносно осі ординат.
, утворюється з графіка функції f перетворенням симетрії відносно осі ординат.
Наслідок 3: графік функції g, що визначається рівністю  де
де 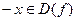 , утворюється з графіка функції f перетворенням симетрії відносно початку координат, тобто послідовного виконання перетворень симетрії відносно осей координат.
, утворюється з графіка функції f перетворенням симетрії відносно початку координат, тобто послідовного виконання перетворень симетрії відносно осей координат.
Користуючись лемами 1 і 2 та наслідками, розглянемо алгоритм побудови графіка функції 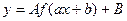 , якщо відомо графік функції
, якщо відомо графік функції 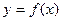 . Для цього перетворимо функцію: у виразі ах+b винесемо за дужки число а, тоді отримаємо
. Для цього перетворимо функцію: у виразі ах+b винесемо за дужки число а, тоді отримаємо 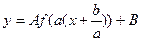 . Позначимо
. Позначимо  , а тоді у=Аf(a(x-α))+B. Отже, щоб побудувати графік функції
, а тоді у=Аf(a(x-α))+B. Отже, щоб побудувати графік функції 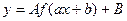 за графіком функції
за графіком функції 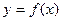 потрібно:
потрібно:
1) перетворити задану функцію до вигляду лем 1 і 2, тобто до виду у=Аf(a(x-α))+B;
2) у системі координат хОу через точку 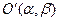 проводимо допоміжні осі координат
проводимо допоміжні осі координат 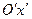 і
і 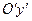 ;
;
3) у системі координат 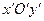 будуємо графік функції
будуємо графік функції  як результат розтягу графіка функції
як результат розтягу графіка функції 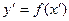 від осі абсцис з коефіцієнтом А і наступного розтягу від осі ординат з коефіцієнтом
від осі абсцис з коефіцієнтом А і наступного розтягу від осі ординат з коефіцієнтом 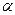 . Побудований графік є шуканим. Проілюструємо сказане на наступних прикладах.
. Побудований графік є шуканим. Проілюструємо сказане на наступних прикладах.
Вправа 1: побудувати графік функції 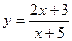 .
.
Дата добавления: 2014-12-03; просмотров: 328; Мы поможем в написании вашей работы!; Нарушение авторских прав |