Сведения из теории. Состояние газа характеризуется тремя величинами - параметрами состояния: давлением Р, объемом V и температурой Т

Состояние газа характеризуется тремя величинами - параметрами состояния: давлением Р, объемом V и температурой Т. Уравнение, связывающее эти величины, называется уравнением состояния газа. Для идеального газа уравнением состояния является уравнение Менделеева-Клапейрона:

,

где М - масса газа; m - масса одного моля; R - универсальная газовая постоянная.

Для одного моля:

PV = RT . (7.1)

Теплоемкостью теланазывается количество теплоты, которое нужно сообщить телу, чтобы изменить его температуру на один градус:

(Дж/К).

Здесь dT - изменение температуры тела при сообщении ему количества теплоты dQ.

Теплоемкость единицы массы тела называется удельной теплоемкостью:

(Дж/(кг·К)).

Теплоемкость одного моля вещества называется молярной теплоемкостью:

(Дж/(моль·К)) . (7.2)

Величина теплоемкости газа зависит от условий его нагревания, т. е. от того, нагревается ли газ при постоянном объеме (обозначим молярную теплоемкость в этом случае через С_v ) или процесс нагревания происходит при постоянном давлении (С_р ). Теплоемкости С_р и С_v связаны между собой. Эту связь можно получить, пользуясь уравнением состояния (7.1), написанным для одного моля газа, и первым началом термодинамики, которое можно сформулировать следующим образом: количество теплоты dQ, переданное системе, затрачивается на увеличение ее внутренней энергии dU и на работу dA, совершаемую системой над внешними телами:

dQ = dU + dA.(7.3)

Элементарная работа

dA = P× dV . (7.4)

Исходя из определения молярной теплоемкости (7.2)

.

При изохорическом процессе V = соnst, следовательно, dV = 0 и dA= 0 (см. формулу (7.4)), поэтому

. (7.5)

При изобарическом процессе Р =соnst,следовательно,

. (7.6)

Из уравнения газового состояния (7.1) получаем

PdV + VdP = RdT.

Но dP = 0 (так как Р = сonst), потому Р dV = R dT. Учитывая это равенство и заменяя dU через С_v dT, из выражения (7.6) получим

С_p = C_v + R. (7.7)

Таким образом С_p > С_v : при нагревании при постоянном давлении тепло, сообщенное газу, идет не только на изменение его внутренней энергии, но и на совершение газом работы.

Важную роль в термодинамике играет величина . В частности, g входит в уравнение Пуассона, описывающее адиабатический процесс, т.е. процесс, протекающий без теплообмена с окружающей средой (dQ = 0). Уравнение Пуассона в переменных Р,Vимеет вид

РV ^g = соnst. (7.8)

Из первого начала термодинамики (7.3) для адиабатического процесса следует:

dU +dA = 0,

откуда

dA = - dU = - C_v dT,

т.е. работа в этом случае совершается за счет изменения запаса внутренней энергии.

Описание установки и метода определения С_р / C_v

Для определения в данной работе используется метод, предложенный немецкими физиками Клеманом и Дезормом.

Установка (рис.7.1) состоит из стеклянного баллона Б емкостью 10 - 15 литров, закрытого пробкой. Через пробку проходят две трубки. Трубка 2 соединена с жидкостным манометром 3, используемым для измерения из­бы­­точного по сравнению с атмо­сфер­ным давления в баллоне. Трубка 1 через кран K₁ соединена с атмо­сфе­рой. Через от­верстие в нижней части бал­лона про­хо­дит третья трубка 5, ко­то­рая че­рез кран K₂ соединяет бал­лон с на­со­сом 4.

Пусть при комнатной темпе­ра­ту­ре Т₁ газ, находящийся в баллоне, имеет давление Р₁ , которое несколько выше атмосферного Р₀. Избыток давления (отсчет h₁ ) можно создать насосом при открытом кране K₂ и измерить манометром 3 (кран K₂ после этого должен быть закрыт), т. е.

Р₁ = Р₀ + h₁ , h₁ << Р₀

Если сейчас на короткое время открыть кран K₁ , то будет иметь место процесс адиабатического расширения газа (теплопроводность стенок баллона мала). Давление газа в баллоне при этом сравняется с атмосферным Р₀ (рис.7.2), а температура газа понизится до Т₂ (работа расширения совершается за счет внутренней энергии газа).

Уравнение Пуассона (7.8), опи­сы­ва­ю­щее адиабатический процесс, в нашем случае удобно записать в переменных Р, Т:

. (7.9)

После процесса расширения в результате теплообмена температура оставшегося в баллоне газа начинает повышаться. Будет повышаться и давление газа, причем до тех пор, пока температура вновь не сравняется с комнатной. Обозначим это давление через Р₂. Очевидно, Р₂ =Р₀ + h₂ , где h₂ << P₀ - избыточное давление, измеренное по манометру в данном случае. Таким образом, сейчас имеет место изохорный процесс нагревания газа со скоростью, определяемой теплопроводностью стеклянных стенок баллона. Как известно, такой процесс подчиняется закону Гей - Люссака:

. (7.10)

Оба процесса (адиабатический, и изохорный ) изображены в координатах Р,V на рис.7.2.

Сравнивая (7.9) и (7.10), можно записать: .

Учитывая, что P₁ = P₀ + h₁ , а Р₂ = P₀ + h₂ , последнее выражение представим как

или

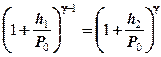. (7.11)

Так как h₁ и h₂ малы по сравнению с Р₀ , то обе части равенства (7.11) можно разложить в ряд. Ограничиваясь членами первого порядка, получаем

,

откуда

. (7.12)

Выражение (7.12) является рабочей формулой для определения g. Как видно, для этого достаточно при проведении опытов измерить h₁ и h₂ .