Дифференциальные уравнения движения системы.

Рас­смотрим систему, состоящую из п материальных точек. Выделим какую-нибудь точку системы с массой . Обозначим равнодейству­ющую всех приложенных к точке внешних сил (и активных и реак­ций связей) через 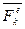, а равнодействующую всех внутренних сил - через . Если точка имеет при этом ускорение , то по основному закону динамики

.

Аналогичный результат получим для любой точки. Следовательно, для всей системы будет:

Эти уравнения, из которых можно определить закон движения каждой точки системы, называются дифференциальными уравнениями движения системы в векторной форме. Уравнения являются дифференциальными, так как ; входящие в правые части уравнений силы будут в общем случае зависеть от времени, координат точек системы и их скоростей.

Проектируя на какие-нибудь координатные оси, мы можем получить дифференциальные уравнения движения системы в проекциях на эти оси.

Полное решение основной задачи динамики для системы состояло бы в том, чтобы, зная заданные силы, проинтегрировать соответ­ствующие дифференциальные уравнения и определить таким путем закон движения каждой из точек системы в отдельности.

Однако такой путь решения обычно не применяется по двум причинам. Во-первых, этот путь слишком сложен и почти всегда связан с непреодолимыми математическими трудностями. Во-вторых, в большинстве случаев при решении задач механики бывает доста­точно знать некоторые суммарные характеристики движения системы вцелом, а не движение каждой из ее точек в отдельности. Эти суммарные характеристики определяются с помощью общих теорем динамики системы, к изучению которых мы и перейдем.

Основная роль уравнений состоит в том, что они, или след­ствия из них, являются исходными для получения соответствующих общих теорем.