Закон сохранения движения центра масс.

Из теоремы о движении центра масс можно получить следующие важные следствия:

1) Пусть сумма внешних сил, действующих на систему, равна нулю

Тогда из уравнения следует, что или Следовательно, если сумма всех внешних сил, действующих на систему, равна нулю, то центр масс этой системы движется с постоянной по модулю и направлению скоростью, т. е. равномерно и прямолинейно. В частности, если вначале центр масс был в покое, то он и останется в покое. Действие внутренних сил, как мы видим, движение центра масс системы изменить не может.

2) Пусть сумма внешних сил, действующих на систему, не равна нулю, но эти силы таковы, что сумма их проекций на какую-нибудь ось (например, ось Ох) равна нулю:

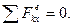
Тогда уравнение дает:

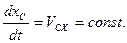
Следовательно, если сумма проекций всех действующих внеш­них сил на какую-нибудь ось равна нулю, то проекция скорости центра масс системы на эту ось есть величина постоянная. В частности, если в начальный момент , то и в любой после­дующий момент , т. е. центр масс системы в этом случае вдоль оси Ох перемещаться не будет (x_C = const).

Все эти результаты выражают собою закон сохранения движе­ния центра масс системы. Рассмотрим некоторые примеры, иллю­стрирующие его приложения.

а) Движение центра масс солнечной системы. Так как притяжением звезд можно практически пренебречь, то можно считать, что на солнечную систему никакие внешние силы не дей­ствуют. Следовательно, в первом приближении ее центр масс дви­жется в мировом пространстве равномерно и прямолинейно.

б) Действие пары сил на тело. Если на свободное твердое тело начнет действовать пара сил , то геометрическая сумма этих внешних сил будет равна нулю . Следовательно, центр масс С тела, если он вначале был неподвижен, должен остаться неподвижным и при действии пары. Таким образом, где бы к свободному твердому телу ни была при­ложена пара сил, тело начнет вращаться вокруг своего центра масс.

в) Движение по горизонтальной плоскости. При отсутствии трения человек с помощью своих мускульных усилий (силы внутренние) не мог бы двигаться вдоль горизонтальной пло­скости, так как в этом случае сумма проекций на любую горизон­тальную ось Ох всех приложенных к человеку внешних сил (сила тяжести и реакция плоскости) будет равна нулю и центр масс человека вдоль плоскости перемещаться не будет (x_C= const).

Если, например, человек вынесет правую ногу вперед, то левая его нога скользнет назад, а общий центр масс останется на месте.

При наличии же трения скольжению левой ноги назад будет пре­пятствовать сила трения, которая в этом случае будет направ­лена вперед. Эта сила и будет той внешней силой, которая позволяет человеку перемещаться в сторону ее действия (в данном случае вперед).

Аналогично происходит движение паровоза или автомобиля. Сила давления пара или газа в двигателе является силой внутренней и сама но себе не может переместить центр масс системы. Движение происхо­дит потому, что двигатель передает соответствующим колесам, назы­ваемыми ведущими, вращающий мо­мент. При этом точка касания В ве­дущего колеса (рис.23) стремится скользить влево. Тогда на колесо будет действовать сила трения, направленная вправо. Эта внешняя

сила и позволит центру тяжести паровоза или автомобиля дви­гаться вправо. Когда этой силы нет или когда она недостаточна для преодоления сопротивления, испытываемого ведомыми колесами, движения вправо не будет; ведущие колеса будут при этом вра­щаться на месте (буксовать).

МОДУЛЬ 7

ЛЕКЦИЯ 13

Модуль 7 состоит из двух лекций, в которых рассматриваются следующие вопросы:

1. Количество движения системы.

2. Теорема об изменении количества движения.

3. Закон сохранения количества движения.

4. Главный момент количеств движения системы.

5. Теорема моментов.

6. Закон сохранения главного момента количеств движения.

7. Кинетическая энергия системы.

8. Некоторые случаи вычисления работы.

9. Теорема об изменении кинетической энергии системы.