ТЕОРИЯ ОПЫТА

Уравнение диффузии для потока тепловых нейтронов

(3)

где - изменение плотности нейтронов в заданном объеме в

единицу времени;

- утечка нейтронов;

- поглощение нейтронов;

S- источник нейтронов.

Стационарное уравнение диффузии для потока Фтепловых нейтронов в среде без источника может быть записано:

(4)

Для тела в форме шара данное уравнение целесообразно переписать в сферических координатах:

. (5)

или

. (6)

С помощью подстановки уравнение (6) легко решается, и его общим решением является

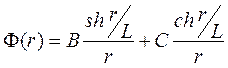, (7)

где В и С - произвольные постоянные, определяемые из гранич­ных условий. Из условия ограниченности нейтронного потока в центре шара (при r = 0) следует, что С= 0. Тогда

. (8)

Константа В может быть найдена из граничного условия на поверхности шара и определяется интенсивностью поверхностного источника тепловых нейтронов. Однако, поскольку в работе проводятся сравнительные измерения, численное значение константы В не требуется. Это равноценно утверждению, что для нахождения величины L не требуется знать абсолютное значение потоки тепловых нейтронов. Но от абсолютной величины потока Ф зависит точность измерения L. Если на опыте определить зависимость Ф(r), сравнить её с аналитическим выражением (8), то можно рассчитать величину диффузии для исследуемого вещества. В простейшем случае достаточно измерить нейтронный поток в двух точках шара r₁ и r₂ и, подставив измеренные значения в уравнение (8), найти L. Нейтронный поток измеряется в единицах активности детектора
нейтронов А :

_. (9)

Здесь A₁ - активность детектора, облученного нейтронами в точ­ке r₁ :

А₂ - то же в точке r₂ . Уравнение (9) является транс­цендентным и решается относительно L либо под­бором величины L , либо графически.