Задачи корреляционного и регрессионного анализа

Понятие корреляция появилось в середине XIX века в работах английских статистиков Ф. Гальтона и К. Пирсона. Термин произошел от латинского «correlatio» – соотношение, взаимосвязь. Термин регрессия (латинское «regressio» - движение назад) также введен Ф. Гальтоном.

В естественных науках часто говорится о функциональной зависимости (связи) двух (или нескольких) переменных, когда каждому возможному значению одной переменной соответствует вполне определенное значений другой.

В экономике в большинстве случаев между переменными величинами существуют такие зависимости, когда каждому значению одной переменной соответствует не какое-то определенное, а множество возможных значений другой переменной, иначе говоря, каждому значению одной переменной соответствует определенное статистическое распределение другой переменной. Такая зависимость получила название статистической (или стохастической, вероятной).

Возникновение понятия статической связи обусловливается тем, что зависимая переменная подвержена влиянию ряда неконтролируемых или неучтенных факторов, а также тем, что измерение значений переменных неизбежно сопровождается некоторыми случайными ошибками.

В силу неоднозначности статистической зависимости между переменными и , в частности, представляет интерес усредненная по схема зависимости, т.е. закономерность в изменении условного математического ожидания 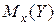в зависимости от (т.е. математического ожидания случайной переменной , вычисленного в предположении, что переменная приняла значение ).

Корреляционной зависимостью между двумя переменными величинами называется функциональная зависимость между значениями одной из них и условными математическим ожиданием другой.

Корреляционная зависимость может быть представлена в виде

(1.1)

Основной задачей регрессионного анализа является установление формы и изучение зависимости между переменными. Основной задачей корреляционного анализа является выявление связи между случайными переменными и оценка ее тесноты.