Корреляционное отношение и индекс корреляции

Коэффициент корреляции, как уже отмечалось, является полноценным показателем тесноты связи лишь в случае линейной зависимости между случайными переменными, имеющими совместное нормальное распределение. Однако часто возникает необходимость в достоверном показателе интенсивности связи при любой форме зависимости.

Для получения такого показателя рассмотрим выборочную дисперсию

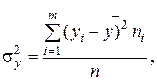
(3.10)

называемую общей дисперсией.

Как известно, если ряд наблюдений переменной состоит из непересекающихся групп, то общая дисперсия может быть представлена в виде суммы двух слагаемых

(3.11)

где 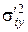– средняя групповых дисперсий 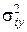, или остаточная дисперсия:

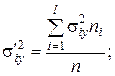
	(3.12)
	(3.13)

– межгрупповая дисперсия:

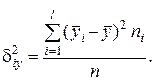
(3.14)

Остаточной дисперсией измеряют ту часть колеблемости , которая возникает из-за изменчивости неучтенных факторов, не зависящих от . Межгрупповая дисперсия выражает ту часть вариации , которая обусловлена изменчивостью . Величина

(3.15)

получила название эмпирического корреляционного отношения по . Чем теснее связь, тем больше влияние на вариацию переменной оказывает изменчивость по сравнению с не уточненными факторами, тем выше . Величина , называемая коэффициентом детерминации, показывает, какая часть общей вариации обусловлена вариацией .

Аналогично вводится эмпирическое корреляционное отношение по :

(3.16)

Основные свойства корреляционных отношений (при достаточно большом объеме выборки ).

1. Корреляционное отношение есть неотрицательная величина, не превосходящая 1:

2. Если 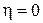, то корреляционная связь отсутствует.

3. Если 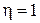, то между переменными существует функциональная зависимость.

4. 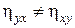, т.е. в отличие от коэффициента корреляции 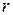(для которого ) при вычислении корреляционного отношения существенно, какую переменную считать независимой, а какую - зависимой.

Эмпирическое корреляционное отношение является показателем степени рассеяния точек корреляционного поля относительно эмпирической линии регрессии, выражаемой ломаной, соединяющей значения . Однако в связи с тем, что закономерное изменение нарушается случайными зигзагами ломаной, возникающими вследствие остаточного действия неучтенных факторов, преувеличивает тесноту связи.

Поэтому наряду с рассматривается показатель тесноты связи 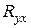, характеризующий рассеяние точек корреляционного поля относительно линии регрессии 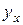. Показатель 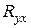получил название теоретического корреляционного отношения, или индекса корреляции по :

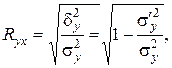
(3.17)

где дисперсии и 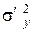определяются по формулам (3.11) – (3.14), в которых групповые средние заменены условными средними 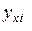вычисленными по уравнению регрессии.

Подобно 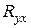вводится и индекс корреляции по :

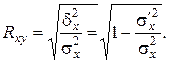
(3.18)

Достоинством рассмотренных показателей и является то, что они могут быть вычислены при любой форме связи между переменными. Хотя и завышает тесноту связи по сравнению с , но для его вычисления не нужно знать уравнение регрессии. Корреляционные отношения и связаны с коэффициентом корреляции 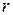следующим образом:

(3.19)

В случае линейной зависимости между переменными 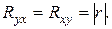Расхождение между и может быть использовано для проверки линейности корреляционной зависимости.

Далее приводится последовательность расчета показателей, оценивающих тесноту корреляционной зависимости, в среде Excel.

1. Для расчета коэффициента корреляции в ячейку B73 записывается формула =(B36*B37)^0,5 (см. рис.5.).

2. Эмпирическое и теоретическое корреляционное отношение по определяются следующим образом (см. рис.5):

· при формировании исходных данных в ячейку A76 записывается формула =C5, в ячейку B76 – формула =I5, в ячейку C76 – формула =J5, в ячейку F76 – формула =C44, после чего все формулы протягиваются по столбцам до 86 строки;

· в ячейку D76 записывается формула =(C76-$B$31)^2*B76 и протягивается до ячейки D86, после чего в ячейке D87 суммируются значения диапазона D76:D86;

· в ячейку G76 записывается формула =(F76-$B$31)^2*B76 и протягивается до ячейки G86, после чего в ячейке G87 суммируются значения диапазона G76:G86;

· для расчета межгрупповых дисперсий в ячейку E88 заносится формула =D87/B87, в ячейку H88 – формула =G87/B87;

· при расчете эмпирического корреляционного отношения в ячейку E89 записывается формула =(E88/B33)^0,5;

· для расчета теоретического корреляционного отношения в ячейку H89 записывается формула =(H88/B33)^0,5.

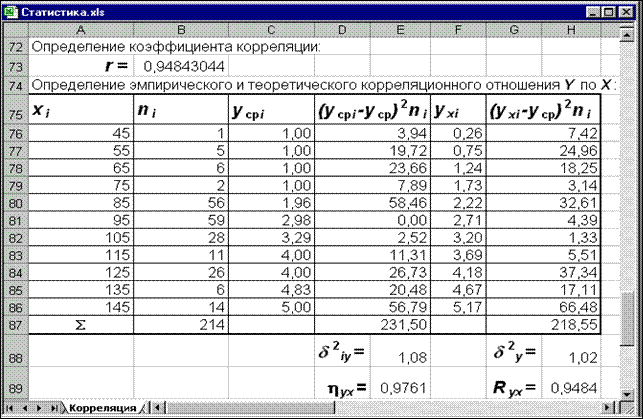
Рис. 5. Экранная форма определения коэффициента корреляции, эмпирического и теоретического корреляционного отношения по

3. При расчете эмпирического и теоретического корреляционного отношения по необходимо выполнить следующее (см. рис.6):

· при формировании исходных данных в ячейку A92 записывается формула =A62, в ячейку С92 – формула =B62, в ячейку F92 – формула =C62, после чего все формулы протягиваются по столбцам до 96 строки;

· для транспонирования значений 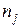выделите диапазон ячеек B92:B96, введите формулу массива =ТРАНСП(D16:H16),нажмите сочетание клавиш CTRL+SHIFT+ENTER;

· в ячейку D92 записывается формула =(C92-$B$30)^2*B92 и протягивается до ячейки D96, после чего в ячейке D97 суммируются значения диапазона D92:D96;

· в ячейку G92 записывается формула =(F92-$B$30)^2*B92 и протягивается до ячейки G96, после чего в ячейке G97 суммируются значения диапазона G92:G96;

· для расчета межгрупповых дисперсий в ячейку E98 заносится формула =D97/B97, в ячейку H98 – формула =G97/B97;

· при расчете эмпирического корреляционного отношения в ячейку E99 записывается формула =(E98/B32)^0,5;

· для расчета теоретического корреляционного отношения в ячейку H99 записывается формула =(H98/B32)^0,5.

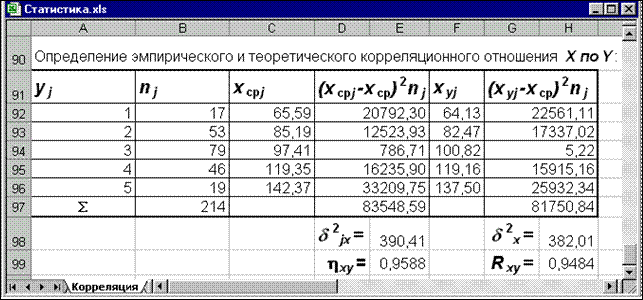
Рис. 6. Экранная форма определения эмпирического и теоретического корреляционного

отношения по