Линейная парная регрессия

Данные о статической зависимости удобно задавать в виде корреляционной таблицы (см. рис.1).

В качестве исходных данных корреляционной таблицы берутся данные факторной группировки, проведенной в предыдущей работе [4].

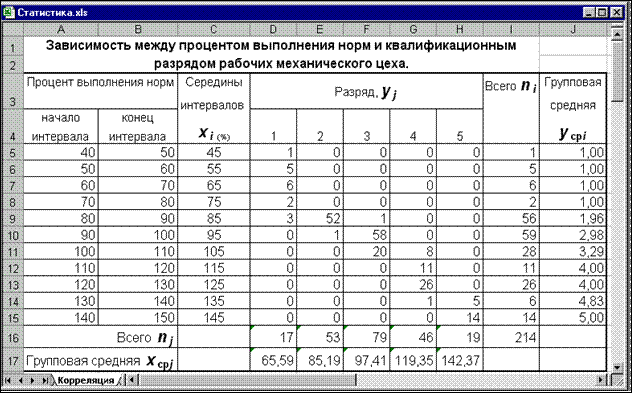
Рис. 1. Исходные данные для решения задач анализа взаимосвязи между двумя переменными

Для каждого значения , т.е. для каждой строки корреляционной таблицы, вычисляются групповые средние :

(2.1)

где – частоты пар

Для этого в ячейку J5 записывается формула =СУММПРОИЗВ($D$4:$H$4;D5:H5)/I5 и протягивается до ячейки J15 включительно.

Аналогично для каждого значения 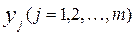по формуле

(2.2)

вычислим групповые средние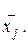

Для этого в ячейку D17 записывается формула =СУММПРОИЗВ($C$5:$C$15;D5:D15)/D16 и протягивается до ячейки H17 включительно.

Вначале предполагается наличие линейной корреляционной зависимости по между двумя рассматриваемыми переменными.

Поэтому уравнение регрессии будем искать в виде

(2.3)

С этой целью применяется метод наименьших квадратов, согласно которому неизвестные параметры и выбираются таким образом, чтобы сумма квадратов отклонений эмпирических групповых средних от ординат , найденных по уравнению регрессии была минимальной:

(2.4)

Параметры и будут определятся из системы нормальных уравнений вида

(2.5)

После некоторых несложных преобразований выражений под знаком суммирования и деления обеих частей уравнений на система нормальных уравнений (2.5) примет вид:

(2.6)

где соответствующие средние определяются по формулам:

	(2.7)
	(2.8)
	(2.9)

Подставляя значение 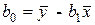из первого уравнения системы (2.6) в уравнение регрессии, получим

или

(2.10)

Коэффициент в уравнении регрессии, называемый коэффициентом регрессии по , будем обозначать символом Теперь уравнение регрессии по запишется так

(2.11)

Коэффициент регрессии по показывает, на сколько единиц в среднем изменяется переменная при увеличении переменной на одну единицу.

Решая систему (2.6) найдем

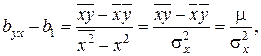
(2.12)

где - выборочная дисперсия переменной :

(2.13)

m - корреляционный момент, или ковариация переменных:

(2.14)

Рассуждая аналогично и задавшись уравнением регрессии в форме

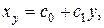
(2.15)

можно привести его к виду

(2.16)

где

(2.17)

– коэффициент регрессии по , показывающий, на сколько единиц в среднем изменяется переменная при увеличении переменной на одну единицу;

(2.18)

– выборочная дисперсия переменной .

Расчетные формулы обобщающих показателей и параметров уравнений регрессии приведены на рис.2.

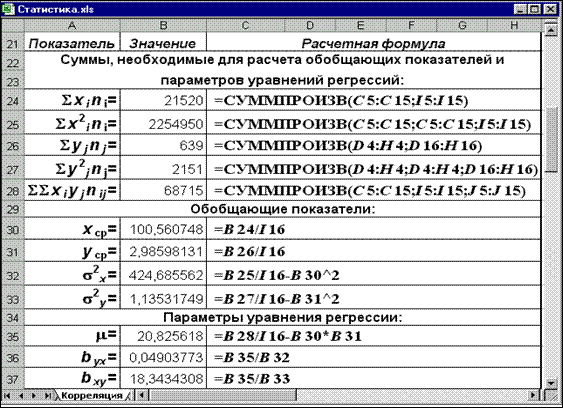
Рис. 2. Экранная форма расчета обобщающих показателей и параметров уравнения регрессии

Далее приводится последовательность построения линий регрессии.

1. При формировании исходных данных для построения эмпирической линии регрессии по в ячейку B44 запишите формулу =J5 и протяните ее до ячейки B54 включительно (см. рис.3).

2. Для определения значений, соответствующих теоретической линии регрессии по , в ячейку C44 запишите формулу =$B$31+$B$36*(A44-$B$30) и протяните ее до ячейки C54 включительно.

3. Выделив диапазон A43:C54, вызовите Мастер диаграмм и выполните все необходимые установки в пошаговом режиме для точечного типа диаграммы.

4. Для формирования исходных данных при построении эмпирической линии регрессии по (см. рис.4):

· выделите диапазон ячеек B62:B66,

· введите формулу массива =ТРАНСП(D17:H17),

· нажмите сочетание клавиш CTRL+SHIFT+ENTER.

5. Для определения значений, соответствующих теоретической линии регрессии по , в ячейку C62 запишите формулу =$B$30+$B$37*(A62-$B$31) и протяните ее до ячейки C66 включительно.

3. Выделив диапазон A61:C66, вызовите Мастер диаграмм и выполните все необходимые установки в пошаговом режиме для точечного типа диаграммы.

Рис. 3. Экранная форма построения эмпирической и теоретической линий регрессии по

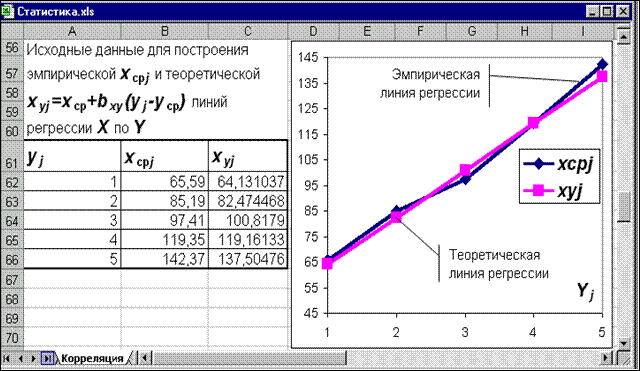
Рис. 4. Экранная форма построения эмпирической и теоретической линий регрессии по