
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Основные виды множественной регрессии
| Наименование формы регрессии | Вид уравнения регрессии |
| Линейная | 
|
| Гиперболическая | 
|
| Параболическая | 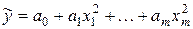
|
| Степенная | 
|
где  – теоретическое значение результативного признака
– теоретическое значение результативного признака  при определенных значениях факторных признаков
при определенных значениях факторных признаков  , подставленных в регрессионное уравнение;
, подставленных в регрессионное уравнение; 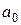 – свободный член уравнения;
– свободный член уравнения;  – коэффициенты множественной регрессии.
– коэффициенты множественной регрессии.
Параметры уравнения множественной регрессии  называют коэффициентами множественной регрессии и определяют с помощью метода наименьших квадратов путем решения системы нормальных уравнений. При этом число нормальных уравнений в общем случае будет равно числу параметров. Если связь отдельного фактора с результатом не является линейной, то производят линеаризацию уравнения. Для упрощения решения системы нормальных уравнений значения всех признаков заменяют на отклонения индивидуальных значений признаков от их средних величин. Полученные коэффициенты множественной регрессии являются именованными числами и показывают, на сколько изменится результативный признак (по отношению к своей средней величине) при отклонении факторного признака от своей средней на единицу и при постоянстве (фиксированном уровне) других факторов.
называют коэффициентами множественной регрессии и определяют с помощью метода наименьших квадратов путем решения системы нормальных уравнений. При этом число нормальных уравнений в общем случае будет равно числу параметров. Если связь отдельного фактора с результатом не является линейной, то производят линеаризацию уравнения. Для упрощения решения системы нормальных уравнений значения всех признаков заменяют на отклонения индивидуальных значений признаков от их средних величин. Полученные коэффициенты множественной регрессии являются именованными числами и показывают, на сколько изменится результативный признак (по отношению к своей средней величине) при отклонении факторного признака от своей средней на единицу и при постоянстве (фиксированном уровне) других факторов.
Значимость коэффициентов множественной регрессии оценивается на основе  критерия Стьюдента.
критерия Стьюдента.  определяют как отношение взятого по модулю коэффициента регрессии к его средней ошибке с заданными уровнем значимости (
определяют как отношение взятого по модулю коэффициента регрессии к его средней ошибке с заданными уровнем значимости (  ) и числом степеней свободы
) и числом степеней свободы 
Коэффициенты регрессии можно преобразовать в сравнимые относительные показатели – стандартизованные коэффициенты регрессии или  коэффициенты (5.1).
коэффициенты (5.1).  коэффициент позволяет оценить меру влияния вариации факторного признака на вариацию результата при фиксированном уровне других факторов.
коэффициент позволяет оценить меру влияния вариации факторного признака на вариацию результата при фиксированном уровне других факторов.

| (5.1) |
где 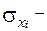 среднее квадратическое отклонение факторного признака,
среднее квадратическое отклонение факторного признака,  – среднее квадратическое отклонение результативного признака,
– среднее квадратическое отклонение результативного признака,  коэффициент регрессии при соответствующем факторном признаке
коэффициент регрессии при соответствующем факторном признаке  .
.
При интерпретации результатов корреляционно-регрессионного анализа часто используют частные коэффициенты эластичности ( 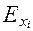 ). Коэффициент эластичности (5.2) показывает, на сколько процентов в среднем изменится значение результативного признака при изменении факторного на 1 % и при постоянстве (фиксированном уровне) других факторов.
). Коэффициент эластичности (5.2) показывает, на сколько процентов в среднем изменится значение результативного признака при изменении факторного на 1 % и при постоянстве (фиксированном уровне) других факторов.

| (5.2) |
где  – среднее значение факторного признака,
– среднее значение факторного признака,  – среднее значение результативного признака.
– среднее значение результативного признака.
Множественная корреляция характеризует тесноту и направленность связи между результативным и несколькими факторными признаками. Основой измерения связей является матрица парных коэффициентов корреляции. По ней можно в первом приближении судить о тесноте связи факторных признаков между собой и с результативным признаком, а также осуществлять предварительный отбор факторов для включения их в уравнение регрессии. При этом не следует включать в модель факторы, слабо коррелирующие с результативным признаком и тесно связанные между собой. Не допускается включать в модель функционально связанные между собой факторные признаки, так как это приводит к неопределенности решения.
Более точную характеристику тесноты зависимости дают частные коэффициенты корреляции. Их удобно анализировать, если они представлены в табличном виде. Частный коэффициент корреляции служит показателем линейной связи между двумя признаками, исключая влияние всех остальных представленных в модели факторов. Например, для двухфакторной модели частный коэффициент корреляции между 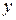 и
и  при фиксированном
при фиксированном  (
(  ) определяется в соответствии с формулой:
) определяется в соответствии с формулой:

| (5.3) |
где  – парные коэффициенты корреляции.
– парные коэффициенты корреляции.
Проверка значимости частных коэффициентов корреляции аналогична, как и для парных коэффициентов корреляции.
Множественный коэффициент корреляции (  )рассчитывается при наличии линейной связи между всеми признаками регрессионной модели.
)рассчитывается при наличии линейной связи между всеми признаками регрессионной модели.  изменяется в пределах от 0 до 1. Значимость множественного коэффициента корреляции проверяется на основе
изменяется в пределах от 0 до 1. Значимость множественного коэффициента корреляции проверяется на основе  критерия Фишера. Например, в двухфакторной модели при оценке связи между результативным и факторными признаками для определения множественного коэффициента корреляции можно использовать формулу:
критерия Фишера. Например, в двухфакторной модели при оценке связи между результативным и факторными признаками для определения множественного коэффициента корреляции можно использовать формулу:

| (5.4) |
где  – дисперсия результативного признака, рассчитанная по регрессионному уравнению;
– дисперсия результативного признака, рассчитанная по регрессионному уравнению;  – общая дисперсия результативного признака;
– общая дисперсия результативного признака; 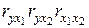 – парные коэффициенты корреляции.
– парные коэффициенты корреляции.
Квадрат множественного коэффициента корреляции называют множественным коэффициентом детерминации  .
. оценивает долю вариации результативного фактора за счет представленных в модели факторов в общей вариации результата.Множественный коэффициент детерминации обычно корректируют на потерю степеней свободы вариации по формуле:
оценивает долю вариации результативного фактора за счет представленных в модели факторов в общей вариации результата.Множественный коэффициент детерминации обычно корректируют на потерю степеней свободы вариации по формуле:
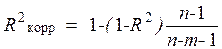
| (5.5) |
где  – корректированный множественный коэффициент детерминации,
– корректированный множественный коэффициент детерминации,  – множественный коэффициент детерминации,
– множественный коэффициент детерминации,  – объем совокупности,
– объем совокупности,  – количество факторных признаков.
– количество факторных признаков.
Статистическая надежность регрессионного уравнения в целом оценивается на основе  критерия Фишера: проверяется нулевая гипотеза о несоответствии представленных регрессионным уравнением связей реально существующим (
критерия Фишера: проверяется нулевая гипотеза о несоответствии представленных регрессионным уравнением связей реально существующим (  ). Для проверки
). Для проверки 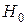 следует расcчитать значение
следует расcчитать значение  критерия (
критерия (  ) и сравнить его с табличным значением (
) и сравнить его с табличным значением (  ) при заданном уровне значимости (
) при заданном уровне значимости (  ) и числе степеней свободы (
) и числе степеней свободы (  и
и  ).
).  определяется из соотношения факторной и остаточной дисперсий, рассчитанных на одну степень свободы по формуле:
определяется из соотношения факторной и остаточной дисперсий, рассчитанных на одну степень свободы по формуле:

| (5.6) |
где  суммы квадратов отклонений, характеризующие факторную и остаточную вариации результативного признака;
суммы квадратов отклонений, характеризующие факторную и остаточную вариации результативного признака;  – число степеней свободы факторной дисперсии;
– число степеней свободы факторной дисперсии;  – число степеней свободы остаточной дисперсии.
– число степеней свободы остаточной дисперсии.
В случае однофакторного дисперсионного комплекса  выражаются в соответствии с формулами:
выражаются в соответствии с формулами:

| (5.7) |
где  – значения результативного признака у
– значения результативного признака у  единицы в
единицы в  й группе,
й группе,  номер единицы совокупности,
номер единицы совокупности,  номер группы,
номер группы,  численность
численность  й группы,
й группы,  средняя величина результативного признака в
средняя величина результативного признака в  й группе,
й группе,  общая средняя результативного признака.
общая средняя результативного признака.
Если , то гипотеза
, то гипотеза 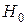 отвергается. При этом с вероятностью
отвергается. При этом с вероятностью  или 95 %принимается альтернативная гипотеза о неслучайной природе оцениваемых характеристик, т.е. признается статистическая значимостьрегрессионного уравнения и его параметров.
или 95 %принимается альтернативная гипотеза о неслучайной природе оцениваемых характеристик, т.е. признается статистическая значимостьрегрессионного уравнения и его параметров.
Рассмотрим возможные процедуры множественной регрессии в среде Excel.
1. Создается новый лист с именем Множественная регрессия, в который копируются данные из листа Исходные данныев диапазонеA2:C215(см. рис.8).
2. Для определения параметров уравнения регрессии в виде  необходимо выполнить следующее (см. рис.9):
необходимо выполнить следующее (см. рис.9):
· выделите диапазон ячеек B218:D222;
· введите формулу массива
=ЛИНЕЙН(C2:C215;A2:B215;ИСТИНА;ИСТИНА) ;
· нажмите сочетание клавиш CTRL+SHIFT+ENTER.
Результат возвращенной функции содержит много полезной информации. В ячейке D218 содержится значение равное коэффициенту уравнения регрессии  , в ячейке C218 – коэффициенту
, в ячейке C218 – коэффициенту  и в ячейке B218–
и в ячейке B218–  . Для того, чтобы определить теоретические значение уровней ряда в ячейку D2 запишите формулу =$D$218+B2*$B$218+A2*$C$218 и протащите по столбцу до 215 строки.
. Для того, чтобы определить теоретические значение уровней ряда в ячейку D2 запишите формулу =$D$218+B2*$B$218+A2*$C$218 и протащите по столбцу до 215 строки.
3. Достоверность аппроксимации может быть оценена с помощью показателя 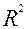 , значение которого будет располагаться в ячейке B220.
, значение которого будет располагаться в ячейке B220.
4. Адекватность выбранного уравнения регрессии оценивается с помощью  – критерия.
– критерия.

Рис. 8. Формирования исходных данных для процедуры множественной регрессии
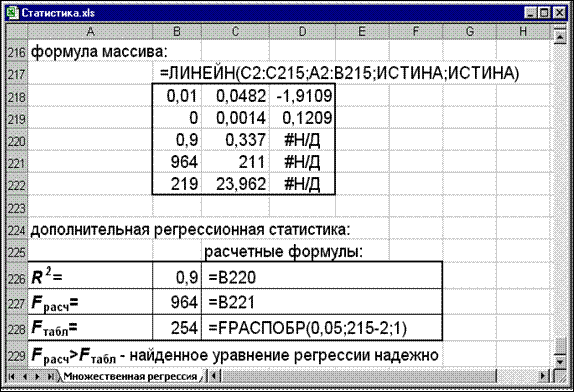
Рис. 9. Экранная форма оценки значимости параметров множественной регрессии
Дата добавления: 2014-12-23; просмотров: 803; Мы поможем в написании вашей работы!; Нарушение авторских прав |