
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Подставляя сюда выражения для химических потенциалов компонента в растворе и в паре, получим

|
| RTlnPi, |
Откуда

|
Если принять активность чистого компонента равной единице, тогда  , так как при
, так как при  . При этом получается соотношение
. При этом получается соотношение
Аналогичное закону Рауля
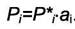
|
(5.18)
Формула (5.18) позволяет определять активности компонентов раствора по измерениям давлений паров над раствором.
Для определения активности можно также использовать измерения осмотического давления, понижения температуры замерзания, повышение температуры кипения раствора и некоторые другие методы. Выношу эти темы для самостоятельного рассмотрения и написания рефератов по конкретным веществам и системам.
Зависимость активности компонента от температуры можно получить при дифференцировании (5.17) по температуре

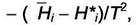
|
| таким образом |
Дата добавления: 2014-12-23; просмотров: 251; Мы поможем в написании вашей работы!; Нарушение авторских прав |