
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Растворах
Рассмотрим раствор, образованный двумя жидкостями, которые смешиваются друг с другом во всём диапазоне концентраций. Если раствор идеален, то суммарное давление паров над раствором равно

|

|

|
| или заменяя |
| ,получим |
| на |

|
т.е. суммарное давление паров над раствором линейно зависит от состава жидкости.
Теперь определим зависимость суммарного давления пара от состава паровой фазы. Состав паровой фазы обозначим штрихом. Тогда

|
Заменим в последней формуле  наи
наи  на
на  . После
. После
преобразований получим: 

откуда

|
(5.21)
Для получения полного давления паров от состава паровой фазы подставим (5.21) в (5.20). После несложных преобразований получаем

|
(5.22)
Из (5.22) видно, что полное давление паров p - нелинейная функция состава пара и изменяется по гиперболе.
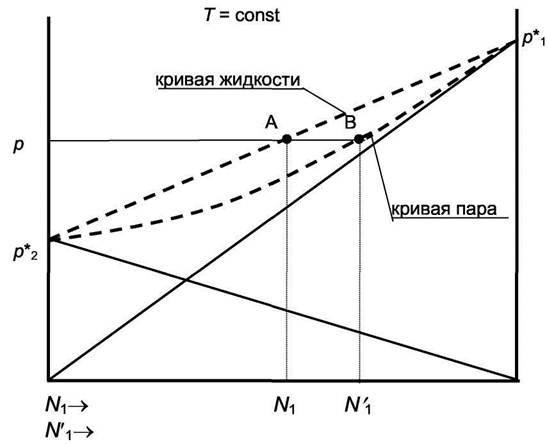
Изобразим рассмотренный пример фазового равновесия пар -раствор на р- N диаграмме для Т= const. (см. рис. 5.2)
|
Рис. 5.2. р - N фазовая диаграмма равновесия пар - жидкость для идеального раствора двух полностью смешивающихся жидкостей.

|

|

|

|
Прямая р*2Ар*1 показывает полное давление, как функцию состава жидкости и называется кривой жидкости. Кривая р*2Вр*1 показывает зависимость полного давления от состава пара и называется кривой пара. Если задать при Т = const некоторое суммарное давление пара р, то этому давлению отвечает жидкость состава N1 (абсцисса точки А) и пар состава N′1 (абсцисса точки В). В условиях равновесия состав жидкости не совпадает с составом пара. В рассмотренном примере пар богаче, чем жидкость более летучим компонентом 1, у которого при данной температуре выше равновесное давление пара. Это положение справедливо только для систем, у которых при изменении состава жидкости полное давление пара меняется монотонно.
Дата добавления: 2014-12-23; просмотров: 290; Мы поможем в написании вашей работы!; Нарушение авторских прав |