
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Реальные растворы. Активности компонентов
Отклонения от идеальности связаны с межмолекулярным взаимодействием компонентов раствора и образованием ассоциатов, сольватов, комплексов. Количественного описания этих сложных взаимодействий нет и теоретический расчёт термодинамических свойств реального раствора пока невозможен. Для этих целей используется эмпирический метод активностей, который аналогичен методу летучестей. Вместо концентраций в термодинамические соотношения вводят величину аi, называемую активностьюкомпонента раствора. Величину ai определяют так, что для реальных растворов остаются справедливыми термодинамические соотношения, полученные для идеальных растворов. Физика взаимодействий, приводящих к отклонению от идеальности, вообще не рассматривается.
Определением активности служит выражение

|
(5.17)
Активность зависит от температуры, давления и состава раствора. Величину отношения аi/Ni = γi называют коэффициентом активности. Коэффициент активности характеризует степень отклонения свойств реального раствора от свойств идеального.
Уравнение (5.17) определяет не абсолютную, а относительную величину активности. Если заданы значения химического потенциала
данного вещества в растворах разного состава (µi)1 и (µi)2, то разность химических потенциалов
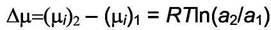
Значит, для определения значений активности компонента в растворе нужны дополнительные условия выбора точки отсчёта. Они могут быть
аналогичны случаю с летучестью, когда принималось, что 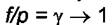 при
при
 . Надо выбрать стандартное состояние, для которого принимается значение
. Надо выбрать стандартное состояние, для которого принимается значение  . Выбор стандартного состояния определяет способ
. Выбор стандартного состояния определяет способ
определения величины  как начальной точки для вычисления
как начальной точки для вычисления
зависимости химического потенциала от состава раствора. Существуют разные системы выбора стандартного состояния для различных типов растворов. Основными являются две системы, так как при  поведение компонента приближается к закону Рауля, а при
поведение компонента приближается к закону Рауля, а при  - к
- к
закону Генри.
Если раствор состоит из жидких компонентов, то можно считать коэффициент активности каждого компонента стремящийся к единице при стремлении к единице его мольной доли. Это так называемая симметричнаясистема отсчёта. Т. е. в уравнении  при
при
 величина
величина 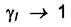 для всех компонентов раствора и
для всех компонентов раствора и  -
-
химический потенциал чистого i-го вещества при стандартном давлении
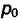
Для ограниченно растворимых веществ, когда одним из компонентов может быть газ или твёрдое тело удобнее применять несимметричнуюсистему отсчёта. В этом случае условия выбора точки отсчёта разные:
Растворитель-  при
при  ;
;
Раств. вещество -  при
при 
Если  при бесконечном разбавлении то величина
при бесконечном разбавлении то величина 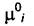 для
для
растворённого вещества представляет собой химический потенциал чистого вещества в гипотетическом стандартном состоянии. В этом состоянии растворённое вещество с концентрацией  имеет свойства, которые оно бы имело в бесконечно разбавленном растворе.
имеет свойства, которые оно бы имело в бесконечно разбавленном растворе.
Рассмотрим пример термодинамического равновесия между компонентом в реальном растворе и паром этого компонента. Условие равновесия
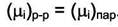
Дата добавления: 2014-12-23; просмотров: 376; Мы поможем в написании вашей работы!; Нарушение авторских прав |