ЦЕЛЬ РАБОТЫ И КРАТКИЕ СВЕДЕНИЯ ИЗ ТЕОРИИ

Коэффициент отражения, или альбедо нейтронов, определяется как отношение тока нейтронов, отраженных от вещества, к току нейтронов, падающих на него (рис. 1 и 2):

,

где ;

.

Рис.1 Рис.2

Альбедо нейтронов есть вероятность отражения нейтронов в результате многократного рассеяния в среде.

Рассмотрим отражение нейтронов на основе диффузионной теории.

Найдем отношение отраженного числа нейтронов, пересекающих за единицу времени единицу площади, к падающему числу нейтронов .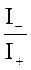

Рис.3

Рассмотрим элементарный кольцевой слой объема , точки которого расположены на расстоянии 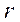от единичной площадки (рис. 3, где - нормаль к площадке ). Число нейтронов, рассеянных в данном слое и достигающих площадки , прямо пропорционально числу рассеивающих столкновений за 1с в объеме , т.е.

,

где анизотропия рассеяния учитывается в транспортном приближении:

;

- полное макроскопическое сечение, ;

- макроскопическое сечение поглощения, ;

- макроскопическое сечение рассеяния, ;

- поток нейтронов,

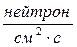
А вероятность того, что нейтрон в результате рассеяния в объеме будет в дальнейшем двигаться в направлении к площадке ,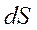

.

Вероятность того, что нейтрон пройдет расстояние 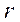без столкновения, определяется так:

.

Учитывая все эти факторы, получаем:

.

Тогда число нейтронов, пересекающих в единицу времени в направлении , будет:

,

где

Для вычисления интеграла выявим значение функции . В этих рассуждениях мы считаем, что не зависит от , а значение потока берем только вблизи площадки, т.е. ограничимся членом первого порядка разложения Маклорена:

В нашем случае берем

или ,

где - значение потока в сечении площадки . Подставив значение потока по этому предположению, будем иметь:

После вычислений интеграла получим:

Аналогично рассуждая можно получить

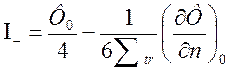
Знак (+) появляется вследствие изменения пределов интегрирования угла .

Выражение называется коэффициентом диффузии.

Альбедо будет иметь выражение .

Так как , то можно записать, разделив числитель и знаменатель на и учтя, что

:

;

1. Если среда (рис.4), генерирующая тепловые нейтроны, отделена плоской границей от безграничного отражателя, в котором распределение потока нейтронов описывается функцией

,

где L - длина диффузии для отражателя, см;

X – расстояние от границы раздела, см ;

то альбедо определяется по следующей формуле:

,

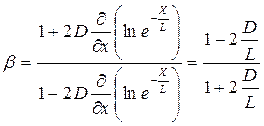Где .

Для изотропного случая Рис.4

.

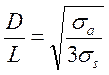Рис.5

2. Если источник имеет форму шара (рис.5), который окружен безграничным отражателем, а распределение потока нейтронов имеет вид

,

где R- расстояние от центра шара до поверхности раздела с отражателем, то альбедо выразится формулой

Альбедо есть средняя вероятность для отдельного нейтрона, упавшего на поверхность вещества, выйти из него назад.

Поскольку угол падения и выхода нейтрона из вещества произволен, то отражение называется диффузионным (равновероятным).

Альбедо зависит от вещества, его толщины, энергии падающих нейтронов и незначительно от угла падения пучка нейтронов, так как “скользящий ”нейтрон совершит первое соударение в среднем ближе к поверхности.

Диффузионная теория даёт значение альбедо в случае бесконечного отражателя, в соответствии с табл.1, при плоской границе раздела.

Таблица 1

Зависимость альбедо от толщины отражателя для плоской задачи даётся формулой

где d – толщина отражателя.

Распределение потока нейтронов с учётом граничного условия при x = d, имеет вид

При x = 0

;

Для бесконечной толщины

и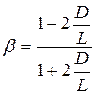

Графически теоретическая зависимость альбедо от толщины отражателя имеет вид, изображённый на рис.6.

Рис.6

При и отражатель можно считать бесконечным.

Как было установлено, для различных энергий нейтронов от одного и того же отражателя альбедо отличается, причём с увеличением энергии нейтронов, падающих на объект, альбедо уменьшается.

Таблица 2

Источник нейтронов	Энергия нейтронов	Альбедо
	0,025	0,38
	0,22	0,30
	0,83	0,12
	5,0	0,07

В табл. 2 дана зависимость альбедо от энергии в геометрии точечного источника, при нормальном падении пучка нейтронов на парафин.

Зависимость интегрального дозового альбедо , определяемого как

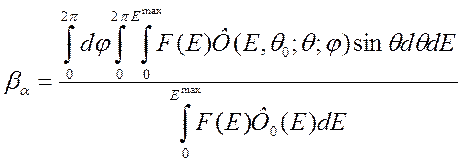
где F(E) – фактор перевода энергии в дозу;

Ф(E; ) – угловое энергетическое распределение плотности потока отражённого излучения;

Ф (E) – поток первичного излучения;

- азимутальный угол отражения рассеянного излучения;

- угол падения плоского мононаправленного пучка на исследуемый отражатель;

- полярный угол отражения рассеянного излучения от угла падения широкого бесконечного пучка нейтронов на барьеры из железа (d=19 см), грунта (d=30 см), воды (d=10 см), показана на графике (рис.7).

1 – железо; 2 – грунт; 3 – вода;

- - - - - расчётная кривая.

Величина интегрального дозового альбедо ( ) для железа и грунта хорошо описывается эмпирической формулой

( )=

где - интегральное дозовое альбедо, =0,86 для железа в случае =0

Исследования зависимости величины интегрального дозового альбедо от толщины железного барьера d показали, что её можно выразить следующим эмпирическим выражением:

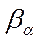
Зависимость ( ) для воды, полиэтилена и парафина можно записать в виде следующего эмпирического соотношения:

( )= .

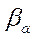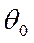Это выражение справедливо при .

Метод

В данном эксперименте используется метод многократного отражения нейтронов от двух парафиновых блоков.

В плоскость раздела между двумя блоками отражателя (замедлителя) помещается детектор тепловых нейтронов (рис.8).

Если - доля нейтронов, поглощённых детектором, то первый отражённый поток нейтронов слабее исходного в 1- раз, так как в результате прохождения через детектор он ослабевает в 1- раз, а при отражении от второго блока в раз. Значит, после первого отражения в активности A добавится активность А(1- ) , в результате последующего А(1- ) и т.д.

Активность за счёт источника одного из блоков после многократного отражения представится в виде суммы ряда

А+ А(1- ) + А(1- ) + . . .=

С учётом обоих блоков суммарная активность

А =

В случае однократного попадания нейтрона в детектор имела бы место формула

А =2А

Усиливающий коэффициент k= ,

Где (1- )=e =e - среднее число попаданий нейтрона в детектор в условиях опыта, когда имеет место многократное отражение.

Альбедо можно вычислить, если найти, эксперименталь Ао и А. На практике нет надобности определять абсолютные активности, достаточно найти пропорциональные им числа импульсов счетчика n и n облученного детектора (рис.9).

В опыте 1 детектор активизируется тепловыми нейтронами из верхнего блока и резонансными из обоих блоков.

Тепловые нейтроны из нижнего блока не достигают детектора, так как поглощаются кадмиевым экраном, а тепловые нейтроны из верхнего блока могут пройти через детектор один раз (однократное прохождение). Аналогично обстоит дело и в опыте 2.

Поправку на активацию детектора резонансными нейтронами можно сделать, воспользовавшись результатами опыта 3, где детектор защищен кадмием с обеих сторон. Мера активности А, наведенной в детекторе тепловыми нейтронами при однократном прохождении через детектор, найдется как среднее значение:

.

В опыте 4 детектор открыт тепловым нейтронам с обеих сторон.

Мерой активности Ао будет при многократном отражении от парафиновых блоков.

Сравнение активностей по числу импульсов возможно, если после каждого опыта детектору дать достаточное время на высвечивание, чтобы не исказить остаточной активностью результаты следующего опыта и если во всех опытах соблюдать одинаковое время активации переноса, счета импульсов, высвечивания.

Экспериментальная установка

Экспериментальная установка состоит из

1) контейнера с парафином и борным поглотителем; внутрь в специальное гнездо вставляется источник 4, мощностью на 1,10

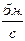
2) парафиновых блоков, место разъема которых отстоит во вставленном состоянии на расстоянии 7 см от источника;

3) серебряной или родиевой пластинок, которые используются в качестве детектора нейтронов.

Серебряная Родиевая

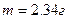
В качестве экрана используется вдвое сложенная кадмиевая пластинка. Экран должен полностью перекрывать детекторы при опытах.

Активность детектора промеряется бета - счётчиком типа МСТ-17 на стандартной установке ПП-8 (см.краткую инструкцию прибора ПП-8).

ПОРЯДОК ВЫПОЛНЕНИЯ ОПЫТОВ

1. Привести в рабочее состояние установку.

а) Включить установку согласно инструкции и прогреть ее в течение 5 минут.

б) Включить пересчетный прибор в режим «Проверка», убедиться в правильности его работы.

в) Установить рабочее напряжение Uр = 1550 В.

2. Измерить величину фона до начала эксперимента (учитывая, что чем больше время измерения фона, тем точнее результаты), время измерения равно 10 мин.

3. Убедиться, что необлученный детектор не изменяет величины фона.

4. Вставить на место разъема парафиновых блоков детектор и кадмиевый экран по условию опыта 1 (экран снизу, детектор сверху).

5. Вставить блоки в контейнер и засекать время по секундомеру. Время облучения 5 мин (родий) и 10 мин (серебро).

6. После облучения блоки вытащить, вынуть детектор и осуществить перенос в свинцовый домик точно за 25 с для серебряного детектора и 40 с для родиевого детектора. От точного соблюдения времени переноса зависит точность результатов измерений.

7. Обсчет детекторов производить в течение 3 мин (родий) и (серебро).

8. По окончании очередного измерения нужно дать детекотру “высветиться”, т.e. довести его активность практически до нуля, чтобы не исказить результаты следующего измерения.

9. Аналогично производятся опыты 2,3,4 в соответствии с их условиями (рис. 9.).

10. Опыты 1,2,3,4 проделать для серебряного и родиевого детекторов.

11. Изменить фон после эксперимента.

12. Выключить установку.

ОБРАБОТКА РЕЗУЛЬТАТОВ ОПЫТА

1. Вычислить для серебряного и родиевого детектора.

2. Найти среднее значение фона.

3. Свести в таблицу результаты опытов и вычислить n и n_0.

4. Из данных опыта вычислить коэффициент диффузионного отражения тепловых нейтронов от парафина _эксп, исходя из формулы

,где

;

;

Na – число Авогадро;

A – атомный вес;

m – масса вещества;

F – площадь пластинки;

для серебряного и родиевого детекторов.

5. Вычислить среднее число попаданий n теплового нейтрона в детектор для каждого случая.

6. Вычислить _теор (теоретическое)_, соответствующие данные взять в литературе, указанной ниже (вычисление произвести для случая плоской задачи).

7. Оценить _эксп (экспeриментальноe) с _теор (теоретическим), сделать вывод.

Таблица 3

Опыт	с фоном	без фона	без фона	n	n0	ЭКСП

ПРАВИЛА ТЕХНИКИ БЕЗОПАСНОСТИ

К ЛАБОРАТОРНОЙ РАБОТЕ № 7

1. В данной работе используется Pu-Be источник

2. Запрещается приступать к выполнению работы без разрешения преподавателя или инженера.

3. Перед началом выполнения работы убедиться в наличии исправного заземления (зануления).

в случае отсутствия заземления (зануления) к работе не приступать и немедленно сообщить об этом преподавателю или инженеру.

4. В процессе выполнения работы не разрешается оставлять рабочее место с включенными приборами без надзора.

5. Запрещается оставлять источник радиоактивного излучения в рабочем положении без облученного детектора.

6. Запрещается подставлять части тела под прямой поток нейронов.

7. Категорически запрещается извлекать источник из лабораторного стенда.

8. ВНИМАНИЕ! На счетчик подается напряжение 1600 В. Касаться токоподводящих частей счетчика категорически запрещается.

9. Запрещается самостоятельно устранять какие бы то ни было неисправности. Обо всех неполадках немедленно сообщать преподавателю или инженеру.

ВОПРОСЫ К РАБОТЕ

1. Определение альбедо.

2. Зависимость альбедо от вещества, его толщины, энергии падающих нейтронов.

3. Как происходит процесс отражения нейтронов?

4. При каком условии отражатель можно считать бесконечным?

5. При каком условии справедливо диффузионное приближение?

6. Что такое

7. Зачем необходимо проводить два измерения: с верхним и нижним размещением кадмия?

8. Что дает измерение, когда детектор покрыт кадмием с обоих сторон?

9. Отличаются ли _экс при использовании в опыте серебряного или родиевого детекторов?

10. Источники нейтронов и их разновидности.

ЛИТЕРАТУРА

1. Роквелл Т. Защита ядерных реакторов/ Пер. с англ. яз.- М.: ИЛ, 1958.

2. Батя Г.А. Основы теории и методов расчета ядерных энергетических реакторов.- М.: Энергоиздат, 1982.

3. Кимель Л.Р. , Машкович В.П. Защита от ионизирующих излучений. – М.: Атомиздат, 1966.

4. Сойгин М.Ф. и др. Судовые ядерные реакторы. – Л.: “Судостроение”, 1967.

5. Горячев И.В. и др. – В сб. “Вопросы физики защиты реакторов”, вып. 3/ Под ред. Д.Л. Бродера и др. – М.: Атомиздат, 1969.

6. Гришкина Т.В. и др. Сборник лабораторных работ по ядерной физике. – М.: Атомиздат, 1970.