
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Нормированная функция Лапласа

| z | |||||||||||
| 0,0 0,1 0,2 0,3 0,4 0,5 0,6 0,7 0,8 0,9 1,0 1,1 1,2 1,3 1,4 1,5 1,6 1,7 1,8 1,9 2,0 2,1 2,2 2,3 2,4 2,5 2,6 | |||||||||||
| z | ||||||||||
| 2,7 2,8 2,9 3,0 3,1 3,2 3,3 3,4 3,5 3,6 3,7 3,8 3,9 4,0 5,0 |
ПРИЛОЖЕНИЕ 3
Значения чисел q в зависимости от объёма выборки n и надёжности  для определения доверительного интервала среднего квадратического отклонения
для определения доверительного интервала среднего квадратического отклонения 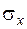
| n | 
| n | 
| |||||||
| 0.95 | 0.99 | 0.999 | 0.95 | 0.99 | 0.999 | |||||
| 0.92 | - | - | 0.32 | 0.49 | 0.73 | |||||
| 0.80 | - | - | 0.28 | 0.43 | 0.63 | |||||
| 0.71 | - | - | 0.26 | 0.38 | 0.56 | |||||
| 0.65 | - | - | 0.24 | 0.35 | 0.50 | |||||
| 0.59 | 0.98 | - | 0.22 | 0.32 | 0.46 | |||||
| 0.55 | 0.90 | - | 0.21 | 0.30 | 0.43 | |||||
| 0.52 | 0.83 | - | 0.188 | 0.269 | 0.38 | |||||
| 0.48 | 0.78 | - | 0.174 | 0.245 | 0.34 | |||||
| 0.46 | 0.73 | - | 0.161 | 0.226 | 0.31 | |||||
| 0.44 | 0.70 | - | 0.151 | 0.211 | 0.29 | |||||
| 0.42 | 0.66 | - | 0.143 | 0.198 | 0.27 | |||||
| 0.40 | 0.63 | 0.96 | 0.115 | 0.160 | 0.211 | |||||
| 0.39 | 0.60 | 0.92 | 0.099 | 0.136 | 0.185 | |||||
| 0.37 | 0.58 | 0.88 | 0.089 | 0.120 | 0.162 | |||||
ПРИЛОЖЕНИЕ 4
Критические точки распределения 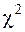
| Число Степеней Свободы | Уровень значимости 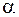
| |||||
| 0,01 | 0,05 | 0,1 | 0,90 | 0,95 | 0,99 | |
| 6,6 9,2 11,3 13,3 15,1 16,8 18,5 20,1 21,7 23,2 24,7 26,2 27,7 29,1 30,6 32,0 33,4 34,8 36,2 37,6 38,9 40,3 41,6 43,0 44,3 45,6 47,0 48,3 49,6 50,9 | 3,8 6,0 7,8 9,5 11,1 12,6 14,1 15,5 16,9 18,3 19,7 21,0 22,4 23,7 25,0 26,3 27,6 28,9 30,1 31,4 32,7 33,9 35,2 36,4 37,7 38,9 40,1 41,3 42,6 43,8 | 2,71 4,61 6,25 7,78 9,24 10,6 12,0 13,4 14,7 16,0 17,3 18,5 19,8 21,1 22,3 23,5 24,8 26,0 27,2 28,4 29,6 30,8 32,0 33,2 34,4 35,6 36,7 37,9 39,1 40,3 | 0,02 0,21 0,58 1,06 1,61 2,20 2,83 3,49 4,17 4,87 5,58 6,30 7,04 7,79 8,55 9,31 10,1 10,9 11,7 12,4 13,2 14,0 14,8 15,7 16,5 17,3 18,1 18,9 19,8 20,6 | 0,004 0,1 0,35 0,71 1,15 1,64 2,17 2,73 3,33 3,94 4,57 5,23 5,89 6,57 7,26 7,96 8,67 9,39 10,1 10,9 11,6 12,3 13,1 13,8 14,6 15,4 16,2 16,9 17,7 18,5 | 0,0002 0,02 0,12 0,30 0,55 0,87 1,24 1,65 2,09 2,56 3,05 3,57 4,11 4,66 5,23 5,81 6,41 7,01 7,63 8,26 8,90 9,54 10,2 10,9 11,5 12,2 12,9 13,6 14,3 15,0 |
ПРИЛОЖЕНИЕ 5
Содержание дисциплины «Математика: Теория вероятностей и математическая статистика»
Тема 1. Сущность и условия применимости теории вероятностей. Основные понятия теории вероятностей
Предмет теории вероятностей. Испытание. Событие. Классификация событий. Классическое, геометрическое, статистическое определение вероятности случайного события. Алгебра событий. Вероятностное пространство. Теоремы сложения и умножения вероятностей. Формула полной вероятности и формула Бейеса. Схема независимых испытаний. Формула Бернулли. Теоремы Муавра-Лапласа. Формула Пуассона.
Дата добавления: 2014-12-23; просмотров: 293; Мы поможем в написании вашей работы!; Нарушение авторских прав |