Решение. По условию задачи число единиц в выборочной совокупности n=400, число единиц, обладающих рассматриваемым признаком m=140

По условию задачи число единиц в выборочной совокупности n=400, число единиц, обладающих рассматриваемым признаком m=140, вероятность Р=0,954.

Из теории вероятностей известно, что при вероятности Р=0,954 коэффициент доверия t=2.

Долю единиц, обладающих указанным признаком, определим по формуле: p=w+∆p, где w = m/n=140/400=0,35=35%,
а предельную ошибку признака ∆p получим из формулы: ∆p= t √w(1-w)/n = 2√0,35×0,65/400 ≈ 0,5 = 5%

Тогда р = 35±5%.

Ответ: Доля бизнес-структур, скрывших часть доходов от уплаты налогов с вероятностью 0,954 равна 35±5%.

25. Ошибки выборочного наблюдения и доверительные пределы генеральной средней (генеральной доли) определяются после того, как получены данные, характеризующие каждую единицу выборочной совокупности. А поэтому при проведении выборки первоначально необходимо определить сколько единиц или какая часть генеральной совокупности должна быть подвергнута наблюдению. Это важный момент в проведении выборочного наблюдения. Важность его в том, что излишняя численность выборочной совокупности вызывает необоснованное завышение затрат времени, труда, материальных и денежных средств, а недостаточная – дает результаты с большей погрешностью. Объем выборки должен быть оптимальным.

Факторами, определяющими численность выборки, являются:

1. Показатели вариации данного признака. Здесь обнаруживается прямая зависимость, т.е. чем больше показатель вариации, тем больше объем выборки.

2. Размер вероятности. Зависимость также прямая. Чем выше вероятность, тем выше коэффициент доверия, а, следовательно, и численность выборки. Величина вероятности зависит от того какое явление изучается. Естественно, что при контроле качества продовольственной продукции величина вероятности выше, чем непродовольственной продукции.

3. Размер возможной допустимой ошибки ( ). Зависимость обратная. Чем меньше размер допустимой ошибки, тем больше должна быть необходимая численность выборки.

4. Способ отбора единиц для обследования. При прочих равных условиях для бесповторной выборки требуется меньшая численность выборки, чем при повторном отборе.

Основной трудностью, возникающей при установлении необходимой численности выборки, является определение среднеквадратического отклонения, которое характеризует вариацию признака. Значение этого показателя отсутствует как для генеральной, так и выборочной совокупности, поскольку задача определения необходимой численности выборки возникает тогда, когда еще выборка не проведена. Поэтому на практике используют несколько методов приближенного расчета среднеквадратического отклонения. Рассмотрим некоторые из них.

1. Вместо среднеквадратического отклонения данного отчетного периода берут значение данного показателя в базисном периоде. Этот прием применяется в тех случаях, когда мы в отчетном периоде, по сравнению с базисным, не ожидаем резкого изменения в исследуемых признаках.

2. Расчет среднеквадратического отклонения может быть основан на той связи, которая существует между показателями средней арифметической и коэффициентом вариации. Практика показывает, что во всех более или менее однородных совокупностях коэффициент вариации колеблется в пределах от 25-35%. Иначе говоря, коэффициент вариации обычно приблизительно равен среднеарифметической величины. А, следовательно, и показатель вариации при расчете необходимой численности выборки будет равен среднеарифметической величины соответствующего признака.

3. Следующий прием опирается на величину размаха вариации. Разность между максимальным и минимальным значениями признака равна приблизительно шести средним квадратическим отклонениям. Разделив размах колебаний на шесть, мы получим приближенное значение среднего квадратического отклонения. Этот прием можно использовать, т.к. максимальное и минимальное значение изучаемого признака известны до проведения наблюдения.

При установлении колеблемости доли, как и средней, в первую очередь надо попытаться найти ориентировочные данные о величине W. Если таких данных нет, то берется максимальная величина произведения W на (1-W). Эта величина равна 0,25.

Необходимую численность выборочной совокупности определяют на основе алгебраического преобразования формулы предельной ошибки выборки для разных видов и способов отбора.

Для собственно-случайной повторной выборки:

.

Чтобы найти численность выборки, нужно освободиться от радикала. Это достигается возведением левой и правой частей уравнения в квадрат.

,

отсюда численность выборки: .

Объем выборочной совокупности прямо пропорционален квадрату коэффициента доверия и дисперсии и обратно пропорционален квадрату предельной ошибки выборки.

При бесповторном собственно-случайном и механическом отборе численность выборки будет равна:

.

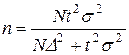Для доли признака численность выборки будет определяться по формулам:

– при повторном отборе,

– при бесповторном отборе.

Аналогичным преобразованием предельной ошибки определяется численность выборочной совокупности при типической и серийной выборке.

Допустим, что для установления средней дневной выработки рабочих предприятия проводится собственно-случайная бесповторная выборка. Сколько рабочих должно быть обследовано, чтобы получить результат с точностью 0,3 р. с вероятностью 0,954. Общая численность рабочих завода 5000 человек. По данным прошлогоднего обследования среднее квадратическое отклонение выработки составляет 1,6 р.

.

Следовательно, должно быть обследовано 112 рабочих, чтобы выполнить поставленные перед наблюдением требования.