
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Оценка достоверности коэффициента корреляции
Дата добавления: 2013-12-12; просмотров: 195; лекция была полезна: 1 студентам(у); не полезна: 0 студентам(у).
| Поделитесь материалом в социальных сетях: |
Пример 2. Определить тесноту взаимосвязи между результатами, показанными легкоатлетами в беге на 100 м, и местом, занятым ими же в соревновании по тройному прыжку. Данные приведены в табл.
| Результат на 100м (х,с) | 10,7 | 10,6 | 10,7 | 10,5 | 10,9 | 10,4 | 10,3 | 10,7 | 10,7 |
| Место в тр.прыжке (у) |
Решение. При решении этой задачи лучше все вычисления постепенно заносить в таблицу.
1. Результаты в беге ранжируем, то есть располагаем их в порядке возрастания:
10,3; 10,4; 10,5; 10,6; 10,7; 10,7; 10,7; 10,7; 10,9.
Для тех результатов, которые повторяются несколько раз, ранг берем как среднее рангов этих результатов. Результат 10,7 повторяется четыре раза, занимая в ряду ранги 5, 6, 7, 8. Тогда
 .
.
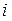
| 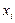
| 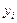
| 
| 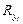
| 
| 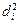
|
| 10,7 | 6,5 | 1,5 | 2,25 | |||
| 10,6 | 4,0 | 2,0 | 4,00 | |||
| 10,7 | 6,5 | 0,5 | 0,25 | |||
| 10,5 | 3,0 | -1,0 | 1,00 | |||
| 10,9 | 9,0 | 6,0 | 36,00 | |||
| 10,4 | 2,0 | -5,0 | 25,00 | |||
| 10,3 | 1,0 | -8,0 | 64,00 | |||
| 10,7 | 6,5 | -1,5 | 2,25 | |||
| 10,7 | 6,5 | 5,5 | 30,25 | |||
| S |
Для  ранг - это занятое место, поэтому
ранг - это занятое место, поэтому 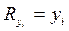 , и 5-й столбец таблицы повторяет 3-й столбец.
, и 5-й столбец таблицы повторяет 3-й столбец.
2. Находим разность рангов: 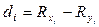 (предпоследний столбец).
(предпоследний столбец).
3. Разность рангов возводим в квадрат и суммируем:  .
.
4. Находим:  .
.
5. Вывод: между исследуемыми признаками существует средне-выраженная отрицательная зависимость, показывающая, что при уменьшении признака 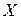 (времени бега на 100 м) результат прыжка в длину увеличивается.
(времени бега на 100 м) результат прыжка в длину увеличивается.
Полученные в примерах коэффициенты корреляции являются выборочными, так как они определены для выборок из соответствующих генеральных совокупностей. Поэтому всегда существует ошибка коэффициента корреляции. Эта ошибка - расхождение между коэффициентом корреляции выборки объемом  и коэффициентом корреляции для генеральной совокупности - определяется формулами:
и коэффициентом корреляции для генеральной совокупности - определяется формулами:
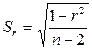 при
при 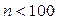 ; и
; и 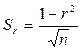 при
при 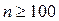 .
.
Оценка достоверности коэффициента линейной корреляции осуществляется с помощью  -критерия Стьюдента:
-критерия Стьюдента:
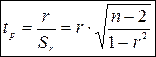 .
.
В данном случае критерий служит для проверки нулевой гипотезы 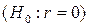 о том, что значение коэффициента корреляции для генеральной совокупности равно нулю, т.е. в генеральной совокупности отсутствует корреляция. Альтернативной является гипотеза
о том, что значение коэффициента корреляции для генеральной совокупности равно нулю, т.е. в генеральной совокупности отсутствует корреляция. Альтернативной является гипотеза 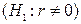 .
.
Критическое значение 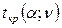 определяется по таблице Стьюдента. Число степеней свободы
определяется по таблице Стьюдента. Число степеней свободы 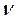 связано с объемом выборки
связано с объемом выборки  формулой:
формулой:
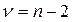 .
.
Если 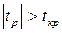 , то нуль-гипотеза отвергается, то есть вычисленный коэффициент корреляции значимо отличается от нуля с вероятностью
, то нуль-гипотеза отвергается, то есть вычисленный коэффициент корреляции значимо отличается от нуля с вероятностью 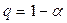 .
.
Пример 3. Коэффициент корреляции между показателями "Толчок штанги" и "Прыжок в высоту с места" для 13 тяжелоатлетов равен 0,855. Требуется оценить достоверность коэффициента корреляции.
Решение. Так как 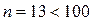 , то для вычисления расчетное значение критерия Стьюдента пользуемся формулой:
, то для вычисления расчетное значение критерия Стьюдента пользуемся формулой:
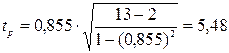 .
.
Задаемся уровнем значимости коэффициента корреляции (вероятность ошибки): 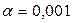 . По формуле находим число степеней свободы:
. По формуле находим число степеней свободы:
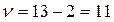 .
.
Из таблицы критических значений распределения Стьюдента следует:
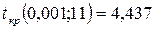 .
.
То есть 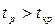 (5,48>4,437). Следовательно, связь между показателями, выраженная коэффициентом корреляции, статистически значима с вероятностью 0,999.
(5,48>4,437). Следовательно, связь между показателями, выраженная коэффициентом корреляции, статистически значима с вероятностью 0,999.
Дата добавления: 2014-12-23; просмотров: 386; Мы поможем в написании вашей работы!; Нарушение авторских прав |