Средне арифметические и средне гармонические индексы и их применение в статистике

В зависимости от методологии расчета индивидуальных и сводных индексов различают средние арифметические и средние гармонические индексы. Другими словами, общий индекс, построенный на базе индивидуального индекса, принимает форму среднего арифметического или гармонического индекса.

Идея построения сводного индекса в виде средней величины из индивидуальных (групповых) индексов вполне естественна, ведь сводный индекс является общей мерой, характеризующей среднюю величину изменения индексируемого показателя, и его величина должна зависеть от величин индивидуальных индексов. А критерием правильности построения сводного индекса в форме средней величины (среднего индекса) является его тождественность агрегатному индексу.

Преобразование агрегатного индекса в средний из индивидуальных (групповых) индексов производится следующим образом: либо в числителе, либо в знаменателе агрегатного индекса индексируемый показатель заменяется его выражением через соответствующий индивидуальный индекс. Если такую замену сделать в числителе, то агрегатный индекс будет преобразован в средний арифметический, если же в знаменателе – то в средний гармонический из индивидуальных индексов.

Формула свободного индекса:

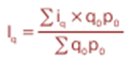
Средний арифметический индекс физического объема, где весами служит стоимость отдельных видов продукции в базисном периоде.

В наличии имеется информация о динамике объема выпуска каждого вида продукции (i_q) и стоимости каждого вида продукции в отчетном периоде (p₁q₁). Для определения общего изменения выпуска продукции предприятия в этом случае удобно воспользоваться формулой Пааше:

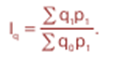
Числитель формулы можно получить суммированием величин p₁q₁, а знаменатель – делением фактической стоимости каждого вида продукции на соответствующий индивидуальный индекс физического объема продукции, т. е. делением p₁q₁/ i_q

Таким образом получаем формулу среднего взвешенного гармонического индекса физического объема.

Применение той или иной формулы индекса физического объема (агрегатного, среднего арифметического и среднего гармонического) зависит от имеющейся в распоряжении информации. Также нужно иметь в виду, что агрегатный индекс может быть преобразован и рассчитан как средний из индивидуальных индексов только при совпадении перечня видов продукции или товаров (их ассортимента) в отчетном и базисном периодах.

▲ 39 Индексы ценные и базисные, с постоянными и переменными весами.

34 Индексы ценные и базисные, с постоянными и переменными весами.
При расчете отдельно взятого индекса веса в числителе и знаменателе относятся к одному и тому же периоду, т.е. всегда одинаковы.
Пусть, например, за ряд периодов имеются данные о каком-то единичном показателе:
В этом случае, веса в вычисляемых индексах могут быть как постоянными (т.е. у всех индексов, относящихся к одному периоду), так и переменными (т.е. изменяющиеся от периода к периоду).
Полученный ряд индексов называется базисными индексами (или коэффициентами роста с постоянной базой).
Теперь будем исчислять ряд индексов как отношение двух соседних уровней. Тогда для периодов II, III, IV, V индексы последовательно будут выражены (с переменной базой)
Полученный ряд индексов называется цепными индексами.
Цепные и базисные индексы с постоянными весами – соизмерителями находятся в следующей взаимосвязи:
Отмечая эту взаимосвязь между цепными и базисными индексами следует иметь в виду, что она должна использоваться с определенными оговорками: для индивидуальных индексов эта взаимосвязь выполняется всегда (безусловно), а для общих индексов будет иметь место только тогда, когда ряд общих индексов рассчитан по одним и тем же весам (т.е. для так называемых индексов с постоянными весами).
Как видели в п. 10.3 настоящей темы, все индексы объемных (количественных) показателей исчисляются по весам – соизмерителям базисного периода, т.е. с постоянными весами. Поэтому к таким индексным рядам указанная взаимосвязь имеет безусловный характер.
В индексном ряду с постоянными весами значительно легче изменять базу расчета.
В то же время все индексы качественных показателей исчисляются по весам – соизмерителям отчетного периода, т.е. являются индексами с переменными весами. Для таких индексных рядов указанная взаимосвязь не выполняется. Однако в статистических исследованиях иногда приходится прибегать к перемножению цепных индексов с переменными весами для того, чтобы получить базисный индекс.

▲ 40 Экономическое содержание индексов.

▲ 41 Взаимосвязь индексов и выявление с их помощью роли отдельных факторов динамики сложных явлений.

36 Взаимосвязь индексов и выявление с их помощью роли отдельных факторов динамики сложных явлений.
Между важнейшими индексами существуют взаимосвязи, позволяющие на основе одних индексов получить другие. Зная, например, значение цепных индексов за какой-либо период времени, можно рассчитать базисные индексы. И наоборот, если известны базисные, то путем деления одного из них на другой можно получить цепные индексы.
Существующие взаимосвязи между важнейшими индексами позволяют выявить влияние различных факторов на изменение изучаемого явления, например связь между индексом стоимости продукции, физического объема продукции и цен. Другие индексы также связаны между собой. Так, индекс издержек производства - это произведение индекса себестоимости продукции и индекса физического объема продукции.
Индекс затрат времени на производство продукции может быть получен в результате умножения индекса физического объема продукции и величины, обратной величине индекса трудоемкости, т.е. индекс производительности труда.
Существует важная взаимосвязь между индексами физического объема продукции и индексами производительности труда.
Индекс производительности труда представляет собой отношение средней выработки продукции (в сопоставимых ценах) в единицу времени (или на одного занятого) в текущем и базисном периодах. Например, индекс физического объема продукции равен произведению индекса производительности труда на индекс затрат рабочего времени (или численности занятых).
Взаимосвязь между отдельными индексами может быть использована для выявления отдельных факторов, оказывающих воздействие на изучаемое явление.