
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Свойства средней арифметической.
Средняя арифметическая обладает некоторыми свойствами, которые определяют ее широкое применение в экономических расчетах и в практике статистического исследования.
Свойство 1.Средняя арифметическая постоянной величины равна этой постоянной:

Свойство 2 (нулевое).Алгебраическая сумма линейных отклонений (разностей) индивидуальных значений признака от средней арифметической равна нулю:
 для первичного ряда и
для первичного ряда и  для сгруппированных данных (di - линейные (индивидуальные) отклонения от средней, т.е. xi -
для сгруппированных данных (di - линейные (индивидуальные) отклонения от средней, т.е. xi -  ).
).
Это свойство можно сформулировать следующим образом: сумма положительных отклонений от средней равна сумме отрицательных отклонений.
Логически оно означает, что все отклонения от средней в ту и в другую сторону, обусловленные случайными причинами, взаимно погашаются.
Свойство 3 (минимальное).Сумма квадратов отклонений индивидуальных значений признака от средней арифметической есть число минимальное:
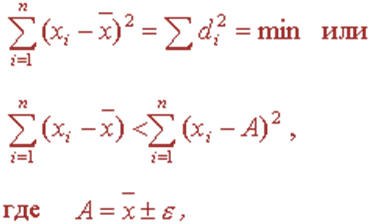
что означает: сумма квадратов отклонений индивидуальных значений признака каждой единицы совокупности от средней арифметической всегда меньше суммы квадратов отклонений вариантов признака от любого значения (А), сколь угодно мало отличающегося от средней у выбранной единицы исследуемой совокупности.
Для сгруппированных данных имеем:

Минимальное и нулевое свойства средней арифметической применяются для проверки правильности расчета среднего уровня признака; при изучении закономерностей изменения уровней ряда динамики; для нахождения параметров уравнения регрессии при изучении корреляционной связи между признаками.
Рассмотренные свойства выражают сущностные черты средней арифметической. Существуют также расчетные (вычислительные) свойства средней арифметической, имеющие прикладное значение:
- если значения признака каждой единицы совокупности (все усредняемые варианты) уменьшить или увеличить на одну и ту же величину А, то и со средней арифметической произойдут аналогичные изменения;
- если значения признака каждой единицы совокупности разделить или умножить на какое-либо постоянное число А, то средняя арифметическая уменьшится или увеличится в А раз;
- если вес (частоту) каждого значения признака разделить на какое-либо постоянное число А, то средняя арифметическая не изменится.
В настоящее время вычислительные свойства средней арифметической потеряли свою актуальность в связи с использованием ЭВМ при расчете обобщающих статистических показателей.
18.Упрощенный способ расчета средней арифметической.
Способ моментов
Часто мы сталкиваемся с расчетом средней арифметической упрощенным способом. В этом случае используются свойства средней величины. Метод упрощенного расчета называется способом моментов, либо способом отсчета от условного нуля.
Способ моментов предполагает следующие действия:
1) Если возможно, то уменьшаются веса.
2) Выбирается начало отсчета – условный нуль. Обычно выбирается с таким расчетом, чтобы выбранное значение признака было как можно ближе к середине распределения. Если распределение по своей форме близко к нормальному, но за начало отсчета выбирают признак, обладающий наибольшим весом.
3) Находятся отклонения вариантов от условного нуля.
4) Если эти отклонения содержат общий множитель, то рассчитанные отклонения делятся на этот множитель.
5) Находится среднее значение признака по следующей формуле
|
| до 70 | -30 | -3 | -45 | ||
| 70-80 | -20 | -2 | -34 | ||
| 80-90 | -10 | -1 | -13 | ||
| 90-100 | |||||
| 100-110 | |||||
| 110-120 | |||||
| 120-130 | |||||
| 130-140 | |||||
| 140 и более | |||||
| Сумма | -12 |
▲ 19 Мода и медиана и их использование в статистике.
Модой распределения называется такая величина изучаемого признака, которая в данной совокупности встречается наиболее часто, т.е. один из вариантов признака повторяется чаще, чем все другие. Мода - значение варьирующего признака, имеющего наибольшую частоту. Мода в интервальном ряду распределения с равными интервалами.
Mo=xMo+iMo*(fMo-f(Mo-1))/((fMo-f(Mo-1))+(fMo-f(Mo-1)) Мода в интервальном ряду с неравными интервалами.
100-120 10 0,5
120-140 30 1,5 <- Mo (мода)
140-180 40 1
180-220 20 0,5
Всего: 100
Для упорядоченного дискретного ряда распределения мода, являющаяся характеристикой вариационного ряда, определяется по частотам вариантов и соответствует варианту с наибольшей частотой.
Медиана – значение варьирующегося признака у той единицы совокупности, которая находится в середине рентированного ряда.
Медиана в дискретном ряду: 23 28 30 35 37 (30 медиана)
Медиана в интервальном ряду распределения: Me = xMe+iMe*(суммаf/2-fиск)/fиск
В дискретном ряду распределения мода определяется визуально. Главное свойство медианы в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины. Квартили представляют собой значение признака, делящее ранжированную совокупность на четыре равновеликие части. Вычисление квартилей аналогично вычислению медианы. Децили – это значение вариант, которые делят ранжированный ряд на десять равных частей: 1-й дециль делит совокупность в соотношении 1/10 к 9/10, 2-й дециль – в соотношении 2/10 к 8/10 и т. д. вычисляются децили по той же схеме, что и медиана, и квартили.
▲ 20 Причины, порождающие вариацию признаков, изучаемых статистикой. Необходимость изучения вариации.
18 Причины, порождающие вариацию признаков, изучаемых статистикой. Необходимость изучения вариации.
При изучении явлений и процессов общественной жизни статистика встречается с разнообразной вариацией (изменчивостью) признаков, характеризующих отдельные единицы совокупности. Величины признаков изменяются под действием различных факторов. Очевидно, что чем разнообразнее условия, влияющие на размер данного признака, тем больше его вариация. Например, размер заработной платы рабочих зависит от нескольких факторов: специальности, разряда, стажа работы, образования, состояния здоровья и т.д. Чем больше различия между значениями факторов, тем больше вариация в уровне заработной платы.
При характеристике колеблемости признака используют систему абсолютных и относительных показателей.
При изучении явлений и процессов общественной жизни статистика встречается с разнообразной вариацией (изменчивостью) признаков, характеризующих отдельные единицы совокупности.
Вариация - это различие в значениях, какого - либо признака у разных единиц данной совокупности в один и тот же момент времени. Величины признаков изменяются под действием различных факторов. И, следовательно, чем разнообразнее условия, влияющие на размер данного признака, тем больше его вариация. Исследование вариации в статистике имеет большое значение, т. к. помогает изучить сущность явления. Измерение вариации, выяснение ее причины, выявление влияния отдельных факторов дает важную информацию (продолжительность жизни, доходы и расходы населения и т. д.) для принятия научно-обоснованных управленческих решений.
▲ 21 Показатели вариации абсолютные и относительные, общие, внутригрупповые и межгрупповые, их смысл и значение. Правило сложения дисперсий.

 19_bilet.png
19_bilet.png
(122.51 КБ) Скачиваний: 0
▲ 22 Среднелинейное отклонение, средний квадрат отклонения (дисперсия), средвнеквадратическое отклонение, коэффициент вариаций.

 23. Математические свойства дисперсии. Упрощенные способы расчета дисперсии
23. Математические свойства дисперсии. Упрощенные способы расчета дисперсии
Дисперсия представляет собой средний квадрат отклонений индивидуальных значений признака от их средней величины и вычисляется по формулам простой и взвешенной дисперсий (в зависимости от исходных данных):
 ,
,
 ,
,
среднее квадратическое отклонение (σ):
 (простое среднеквадратическое отклонение),
(простое среднеквадратическое отклонение),
 (взвешенное среднеквадратическое отклонение).
(взвешенное среднеквадратическое отклонение).
Среднее квадратическое отклонение – это обобщающая характеристика размеров вариации признака в совокупности. Оно выражается в тех же единицах, что и признак.
Расчет дисперсии может быть упрощен. В случае равных интервалов в вариационном ряду распределения используется способ отсчета от условного нуля (способ моментов). Для его понимания необходимо знать следующие свойства дисперсии:
Свойство 1. Дисперсия постоянной величины равна нулю.
Свойство 2. Уменьшение всех значений признака на одну и ту же величину A не меняет величины дисперсии  .Значит, средний квадрат отклонений можно вычислить не по заданным значениям признака, а по отклонениям их от какого-либо постоянного числа.
.Значит, средний квадрат отклонений можно вычислить не по заданным значениям признака, а по отклонениям их от какого-либо постоянного числа.
Свойство 3. Уменьшение всех значений признака в K раз уменьшает дисперсию в K2 раз, а среднее квадратическое отклонение в K раз  .Значит, все значения признака можно разделить на какое-то постоянное число, например, на величину интервала ряда, исчислить среднее квадратическое отклонение, а затем умножить его на постоянное число:
.Значит, все значения признака можно разделить на какое-то постоянное число, например, на величину интервала ряда, исчислить среднее квадратическое отклонение, а затем умножить его на постоянное число:  .
.
Свойство 4. Если вычислить средний квадрат отклонений от любой величины A, в той или иной степени отличающейся от средней арифметической (), то он всегда будет больше среднего квадрата отклонений, вычисленного от средней арифметической  .Средний квадрат отклонений при этом будет больше на величину ( – A)2 :
.Средний квадрат отклонений при этом будет больше на величину ( – A)2 :
 .
.
Значит, дисперсия от средней величины всегда меньше дисперсий, вычисленных от любых других величин, т.е. она имеет свойство минимальности.
На этих математических свойствах дисперсии основываются способы, которые позволяют упростить ее вычисление. Например, расчет дисперсии по способу моментов или способу отсчета от условного нуля применяется в вариационных рядах с равными интервалами. Расчет производится по формуле:
 ,
,
где K – ширина интервала;
A – условный нуль, в качестве которого удобно использовать середину интервала, обладающего наибольшей частотой;
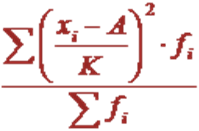 – момент второго порядка.
– момент второго порядка.
Между средним линейным и средним квадратическим отклонениями существует примерное соотношение  если фактическое распределение близко к нормальному.
если фактическое распределение близко к нормальному.
В условиях нормального распределения существует следующая зависимость между величиной среднего квадратического отклонения и количеством наблюдений:
1) в пределах ± 1σ располагается 68,3 % количества наблюдений;
2) в пределах ± 2σ – 95,4 %;
3) в пределах ± 3σ – 99,7 %;
В действительности, на практике почти не встречаются отклонения, которые превышают ±3σ. Отклонение 3σ может считаться максимально возможным. Это положение называют «правилом трех сигм».
▲ 24 Дисперсия альтернативного признака.
21 Дисперсия альтернативного признака.
Альтернативный признак – это признак, характеризующий обладание или не обладание чем-то ( см.п.1.2.).
В статистике при изучении вариации альтернативных признаков наличия изучаемого признака обозначаются «1», а его отсутствие – «0».
Доля единиц совокупности, обладающих изучаемым признаком – «p” , а не обладающих им “q”, следовательно, p + q = 1
Дисперсия альтернативного признака равна произведению доли на дополняющее эту долю до единицы число. Корень квадратный из этого показателя соответствует среднему квадратическому отклонению альтернативного признака.
Показатели вариации альтернативных признаков широко используются в статистике, в частности при проектировании выборочного наблюдения, обработке данных социологических обследований, статистическом контроле качества продукции, в ряде других случаев.
▲ 25 Выборочное наблюдение, значение и условия применения.
22 Выборочное наблюдение, значение и условия применения.
статистическое наблюдение, при котором исследованию подвергают не все элементы изучаемой совокупности (называемой при этом «генеральной»), а только некоторую, определённым образом отобранную их часть. Отобранная часть элементов совокупности (выборка) будет представлять всю совокупность с приемлемой точностью при двух условиях: она должна быть достаточно многочисленной, чтобы в ней могли проявиться закономерности, существующие в генеральной совокупности; элементы выборки должны быть отобраны объективно, независимо от воли исследователя, так чтобы каждый из них имел одинаковые шансы быть отобранным или же чтобы шансы эти были известны исследователю. Эти условия устанавливаются математической теорией выборочного метода. Она основана на ряде важнейших теорем теории вероятностей, составляющих так называемый закон больших чисел (см. Больших чисел закон). Лишь при соблюдении этих условий возникает объективная возможность оценить точность Выборочное наблюдение на основании самих выборочных данных. Точность Выборочное наблюдение измеряется с помощью средней ошибки выборки, величина которой прямо пропорциональна степени вариации изучаемых признаков и обратно пропорциональна объёму выборки. Выборочное наблюдение можно произвести быстрее сплошного, с меньшими затратами и получить результаты, по точности мало уступающие результатам сплошного наблюдения, а с учётом же возможности более тщательного наблюдения — даже нередко превосходящие их.
▲ 26 Ошибки выборочного наблюдения.
23 Ошибки выборочного наблюдения.
Между признаками выборочной совокупности и признаками генеральной совокупности, как правило, существует некоторое расхождение, которое называют ошибкой статистического наблюдения. При массовом наблюдении ошибки неизбежны, но возникают они в результате действия различных причин. Величина возможной ошибки выборочного признака слагается из ошибок регистрации и ошибок репрезентативности. Ошибки регистрации, или технические ошибки, связаны с недостаточной квалификацией наблюдателей, неточностью подсчетов, несовершенством приборов и т. п.
Под ошибкой репрезентативности (представительства) понимают расхождение между выборочной характеристикой и предполагаемой характеристикой генеральной совокупности. Ошибки репрезентативности бывают случайными и систематическими.
Систематические ошибки связаны с нарушением установленных правил отбора. Случайные ошибки объясняются недостаточно равномерным представлением в выборочной совокупности различных категорий единиц генеральной совокупности
. В результате первой причины выборка легко может оказаться смещенной, так как при отборе каждой единицы допускается ошибка, всегда направленная в одну и ту же сторону. Эта ошибка получила название ошибки смещения. Ее размер может превышать величину случайной ошибки. Особенность ошибки смещения состоит в том, что, представляя собой постоянную часть ошибки репрезентативности, она увеличивается с увеличением объема выборки. Случайная же ошибка с увеличением объема выборки уменьшается. Кроме того, величину случайной ошибки можно определить, тогда, как размер ошибки смещения непосредственно практически определить очень сложно, а иногда и невозможно. Поэтому важно знать причины, вызывающие ошибку смещения, и предусмотреть мероприятия по ее устранению.
▲ 27 Методы определения ошибки выборки для средней и для частости, при различных способах и методах отбора.
24 Методы определения ошибки выборки для средней и для частости, при различных способах и методах отбора.
-Отклонение результатов, полученных с помощью выборочного наблюдения от истинных данных генеральной совокупности.
Ошибка выборки бывает двух видов – статистическая и систематическая. Статистическая ошибка зависит от размера выборки. Чем больше размер выборки, тем она ниже.
▲ 28 Определение численности выборки.
25 Определение численности выборки.
Определение необходимого объема выборки – это важная задача, с которой сталкивается исследователь, организующий выборочное наблюдение.
При этом ему, как правило, известно: какие характеристики генеральной совокупности он хотел бы оценить, какую величину ошибки он считал бы несущественной, какой метод выбора данных он использует. Известно также расположение генеральной совокупности и часто (но не всегда) количество элементов в ней.
Расчет численности выборки основывается на статистическом подходе обработки данных и за ним стоит множество вычислений, но для простоты, ниже мы представим формулу, следуя которой можно достичь хороших результатов.
Дата добавления: 2014-12-23; просмотров: 2888; Мы поможем в написании вашей работы!; Нарушение авторских прав |