
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
УДК 070(075.8) ББК 76.01я73 С 24 2 страница
Масштаб графика – это мера перевода численной величины в графическую (например, 1 см соответствует 100 тыс. руб.); чем длиннее отрезок линии, принятой за числовую единицу, тем крупнее масштаб.
Масштабной шкалой является линия, отдельные точки которой читаются как определенные числа. Шкала, по которой отсчитываются уровни изучаемых показателей, как правило, начинается с нуля. Последнее число, наносимое на шкалу, несколько превышает максимальный уровень, отсчет которого проводится по этой шкале. При построении графика допускается разрыв масштабной шкалы. Этот прием используется для изображения статистических данных, имеющих значения лишь в определенных значениях.
Экспликация графика – это пояснение его содержания. Экспликация включает в себя заголовок графика, объяснения масштабных шкал, пояснения отдельных элементов графического образа.
Заголовок графика в краткой и четкой форме отражает основное содержание изображаемых данных. Помимо заголовка на графике дается текст, делающий возможным чтение графика. Цифровые обозначения шкалы дополняются указанием единиц измерения.
7.3. КЛАССИФИКАЦИЯ СТАТИСТИЧЕСКИХ ГРАФИКОВ
При всем своем многообразии статистические графики в курсе «Статистика» классифицируются по ряду признаков: способу построения, форме применяемых графических образов, характеру решаемых задач.
По способу построения статистические графики подразделяются на диаграммы, картограммы и картодиаграммы.
Диаграмма представляет собой чертеж, на котором статистическая информация изображается посредством геометрических фигур или символических знаков.
Диаграмма сравнения показывает соотношение признака статистической совокупности. Каждое значение изучаемого показателя изображается в виде вертикального столбика. Количество столбиков определяется числом изучаемых показателей (данных). Расстояние между столбиками должно быть одинаковым. У основания столбиков дается название изучаемого показателя.
Секторная диаграмма строится таким образом, чтобы каждый сектор занимал площадь круга пропорционально удельному весу отображаемых частей целого
Статистическая карта – вид графика, который иллюстрирует содержание статистических таблиц, где подлежащим является административное или географическое деление совокупности. На лист изображения наносится контурная географическая карта, отражающая деление совокупности на группы. Статистическая карта называется картограммой, вся информация на ней отображается в виде штриховки, линий, точек, окраски, отражающих изменение какого-либо показателя.
На картодиаграмме на фоне карты присутствуют элементы диаграммных фигур. Преимущество картодиаграммы перед диаграммой состоит в том, что она не только дает представление о величине изучаемого показателя на различных территориях, но и изображает пространственное размещение изучаемого показателя.
При обработке и отображении экспериментальных данных, в которых изучаемый признак может принимать любое значение из некоторого интервала, используют следующие способы представления данных:
■ гистограмма;
■ полигон частот;
■ полигон накопленных частот (кумулята).
Гистограмма состоит из примыкающих друг к другу прямоугольников, изображенных на координатной сетке.
Полигон частот – ломаная линия, соединяющая точки, соответствующие срединным значениям интервалов группировки и частотам интервалов.
Полигон частот получается из гистограммы, если соединить середины вершин прямоугольников ломаной линией.
Полигон накопительных частот. В данном случае для построения используются накопленные частоты.
ТРЕБОВАНИЯ К ПОСТРОЕНИЮ СТАТИСТИЧЕСКИХ ГРАФИКОВ
Все буквенные и цифровые значения должны располагаться на графике так, чтобы их легко можно было отсчитать от начала масштабной шкалы. Ряды цифровых данных, отображающие изменения показателей коммерческой деятельности во времени, размещаются в строгой хронологической последовательности и обязательно по оси абсцисс.
Общим требованием графического метода изображения статистических показателей является то, что факторные признаки размещаются на горизонтальной шкале графика и их изменения читаются слева направо, а результативные признаки – по вертикальной шкале и читаются снизу вверх. Это повышает аналитическое значение статистических графиков. Важно, чтобы заголовок графика был бы кратким, но достаточно четко пояснял основное его содержание.
8.1. ПОНЯТИЕ И КЛАССИФИКАЦИЯ РЯДОВ ДИНАМИКИ
Ряды динамики – это статистические данные, отображающие развитие изучаемого явления во времени.
Ряд динамики состоит из двух элементов: в нем указываются моменты времени (обычно дата) или периоды времени (год, квартал, месяц, сутки), к которым относятся приводимые статистические данные и статистические показатели – уровни ряда, характеризующие состояние явления на указанный момент или за период.
Ряды динамики классифицируют следующим образом.
1.В зависимости от способа выражения уровней различают ряд абсолютных величин, ряд средних величин, ряд относительных величин.
2.В зависимости от того, как уровни ряда отражают состояние явления: на определенные моменты времени (начало месяца, квартала, года и т.п.) или за определенные интервалы времени (за сутки, месяц, год и т.п.), различают соответственно моментные и интервальные ряды динамики.
3.В зависимости от расстояния между уровнями ряды динамики могут быть с равноотстоящими уровнями и неравно отстоящими уровнями во времени.
4.В зависимости от наличия основной тенденции изучаемого процесса ряды динамики бывают стационарными и нестационарными.
5.По числу показателей можно выделить изолированные и комплексные (многомерные) ряды динамики.
Сопоставимость уровней рядов динамики. Уровни ряда динамики должны быть сопоставимы по методологии учета и расчета показателей, территориальным границам, кругу охватываемых объектов, единицам измерения и другим признакам. В тех случаях, когда уровни ряда динамики оказываются несопоставимы между собой, их необходимо привести к сопоставимому виду, применяя прием, который называют смыканием рядов динамики.
Для количественной оценки динамики социально-экономических явлений применяются следующие статистические показатели: абсолютный прирост, темп роста, темп прироста, абсолютное значение одного процента прироста.
Средние показатели ряда динамики являются обобщающей характеристикой его абсолютных уровней, абсолютной скорости и интенсивности изменения уровней ряда динамики.
Различают следующие средние показатели: средний уровень ряда динамики, средний абсолютный прирост, средний темп роста и прироста.
Методы расчета среднего уровня ряда динамики зависят от его вида и способов получения статистических данных.
Выявление основной тенденции ряда динамики. При изучении в рядах динамики основной тенденции развития явления применяются различные приемы и методы: метод укрупнения интервалов, метод скользящей средней, метод аналитического выравнивания.
Наиболее эффективный метод выявления основной тенденции развития – аналитическое выравнивание. В этом случае уровни ряда динамики выражаются в виде функции времени: yt = f(t).
Аналитическое выравнивание может быть осуществлено по любому рациональному многочлену. Функция выбирается на основе анализа характера закономерности динамики данного явления.
Колеблемость динамических рядов. Основная тенденция показывает, как систематические факторы воздействуют на уровень ряда динамики, а колеблемость уровней тренда служит мерой воздействия остаточных факторов.
Мерой колеблемости динамического ряда выступает средний квадрат отклонений фактических уровней, исчисленных по тренду. Ее можно измерить показателем среднего квадратического отклонения.
Относительной мерой колеблемости является коэффициент вариации, равный отношению среднего квадратического отклонения к среднему уровню ряда.
Измерение сезонных колебаний. При анализе рядов динамики важное значение имеет выявление сезонных колебаний. Этим колебаниям свойственны более или менее устойчивые изменения уровней ряда по инутригодовым периодам: месяцам, кварталам. Для выявления сезонных колебаний обычно анализируются месячные и квартальные уровни ряда динамики за год или несколько лет. При изучении сезонных колебаний используются специальные показатели – индексы сезонности (Is):

где  – средняя для каждого месяца за изучаемый период;
– средняя для каждого месяца за изучаемый период;
 – общий средний месячный уровень за изучаемый период.
– общий средний месячный уровень за изучаемый период.
Совокупность исчисленных для каждого годового цикла индексов сезонности характеризует сезонную волну развития явления во внутригодовой динамике и наглядно может быть представлена графическим методом. При наличии ярко выраженной тенденции развития (увеличение или уменьшение уровней из года в год) применимы другие способы измерения сезонных колебаний, в частности, индексы сезонности определяются на основе методов, которые позволяют исключать влияние тенденции роста (падения).
В таких случаях фактические данные сопоставляются с выравненными, и индексы сезонности определяются по формуле

где  – исходные уровни ряда;
– исходные уровни ряда;
 – выравненные (теоретические) уровни ряда; п – число годовых периодов.
– выравненные (теоретические) уровни ряда; п – число годовых периодов.
Выравнивание может быть проведено методом аналитического выравнивания или методом скользящей средней.
8.2. СТАТИСТИЧЕСКИЕ ПОКАЗАТЕЛИ РЯДА ДИНАМИКИ
Пример 1. Имеются следующие данные о динамике производства тканей в одном из регионов за 1999–2003 гг.
| Год | Производство тканей, млн м2 | Абсолютный прирост, млн м2 | Темп роста, % | Темп прироста, % | Абсолютное значение | ||||
| по сравнению с предыдущим годом | по сравнению с 1999 г. | по сравнению с предыдущим годом | по сравнению с 1999 г. | 1% прироста, млн м2 | |||||
| по сравнению с предыдущим годом | по сравнению с 1999 г. | ||||||||
| - | - | - | 100,0 | - | - | - | |||
| 104,3 | 104,3 | 4,3 | 4,3 | 2,56 | |||||
| 104,5 | 109,0 | 4,5 | 9,0 | 2,67 | |||||
| 104,3 | 113,7 | 4,3 | 13,7 | 2,79 | |||||
| 104,8 | 119,1 | 4,8 | 19,1 | 2,91 | |||||
| Итого | - | - | - | - | - | - |
Аналитические показатели уровня ряда получаются сравнением уровней между собой.
Сравниваемый уровень принято называть текущим, а уровень, с которым происходит сравнение,– базисным. За базу сравнения обычно принимают предыдущий уровень или начальный уровень ряда динамики.
При сравнении каждого уровня с предыдущим получаются цепные показатели.
Если же сравнение ведется с одним уровнем (базой), то показатели называются базисными.
Для выражения абсолютной скорости роста (снижения) уровня ряда динамики исчисляют статистический показатель – абсолютный прирост ( 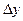 ). Его величина определяется как разность двух сравниваемых уровней и вычисляется следующим образом:
). Его величина определяется как разность двух сравниваемых уровней и вычисляется следующим образом:
 – базисные показатели;
– базисные показатели;
 – цепные показатели,
– цепные показатели,
где  – уровень i-го периода (кроме первого); у0 – уровень базисного периода;
– уровень i-го периода (кроме первого); у0 – уровень базисного периода;  – уровень предыдущего периода.
– уровень предыдущего периода.
В примере 1 абсолютный прирост по сравнению с 1999 г. составит:
■ в 2000 г.-Dy= 267 - 256= 11 (млн м2);
■ в 2001 г. - Dy - 279 - 256 = 23 (млн м2) и т.д.
Цепные показатели абсолютного прироста для примера 1. Абсолютный прирост составит:
■ в 2000 г. по сравнению с 1999 г.- Dy = 267 - 256 = 11 (млн м2);
■ 2001 г. по сравнению с 2000 г. - Dy = 279 - 267 = 12 (млн м2) и т.д.
Интенсивность изменения уровней ряда динамики оценивается отношением текущего уровня к предыдущему или базисному.
Этот показатель называется коэффициентом роста, или темпом роста (Гр), и выражается в процентах:
 – базисные показатели;
– базисные показатели;
 – цепные показатели.
– цепные показатели.
Если Тр больше 100%, уровень растет, если меньше - уровень уменьшается. Тр – всегда положительное число. В примере 1 темп роста составит:
■ в 2000 г. по сравнению с базисным 1999 г. – 
■ в 2001 г. по сравнению с базисным 1999 г. –  и т.д.
и т.д.
Рассчитаем цепные показатели темпа роста для примера 1. Темп роста составит:
■ в 2000 г. по сравнению с базисным 1999 - 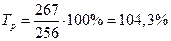
■ в 2001 г. по сравнению с 2000 г. – 
Для выражения изменения величины абсолютного прироста уровней ряда динамики в относительных величинах определяется темп прироста (Тпр), который рассчитывается как отношение абсолютного прироста к базисному или предыдущему уровню:
 – базисные показатели;
– базисные показатели;
 – цепные показатели.
– цепные показатели.
Показатель абсолютного значения 1% прироста (|%|) определяется как результат деления абсолютного прироста на соответствующий темп прироста, выраженный в процентах.
 , или
, или  .
.
В примере 1 абсолютное значение прироста 1% составит:
■ в 2000 г. по сравнению с 1999 г. -  (млн. м2);
(млн. м2);
■ в 2001 г. по сравнению с 2000 г. -  (млн. м2) и т.д.
(млн. м2) и т.д.
8.3. МЕТОД СКОЛЬЗЯЩЕЙ СРЕДНЕЙ
Покажем применение скользящей средней на следующем примере.
Пример 4. На основе данных об урожайности зерновых культур в хозяйстве за 1989–2003 гг. проведем сглаживание ряда методом скользящей средней.
Динамика урожайности зерновых культур в
хозяйстве за 1989–2003 гг. и расчет скользящих средних
| Год | Урожайность зерновых, ц/га | Трехлетние скользящие суммы | Трехлетние скользящие средние | 4-летние скользящие суммы | 4-летние скользящие средние (нецентри- рованные) | 4-летние скользящие средние (центри- рованные) |
| 19,5 | - | - | - | - | - | |
| 23,4 | - | 22,6 | - | 22,5 | - | |
| 25,0 | 67,9 | 23,6 | - | 24,1 | 23,3 | |
| 22,4 | 70,8 | 24,3 | 90,3 | 25,4 | 24,8 | |
| 25,5 | 72,9 | 25,6 | 96,3 | 25,8 | 25,6 | |
| 28,8 | 76,7 | 27,0 | 101,7 | 27,8 | 26,8 | |
| 26,6 | 80,9 | 28,6 | 103,3 | 26,6 | 27,2 | |
| 30,4 | 85,8 | 25,9 | 111,3 | 28,4 | 27,5 | |
| 20,7 | 77,7 | 29,0 | 106,5 | 30,7 | 26,6 | |
| 35,8 | 86,9 | 30,8 | 113,5 | 29,5 | 30,3 | |
| 36,0 | 92,5 | 32,5 | 122,9 | 32,5 | 31,0 | |
| 25,6 | 97,4 | 31,4 | 118,1 | 32,3 | 32,4 | |
| 32,5 | 94,1 | 31,0 | 129,9 | 30,1 | 31,2 | |
| 35,0 | 94,7 | 31,6 | 129,1 | - | - | |
| 27,2 | 94,7 | - | 120,3 | - | - |
По графе 5 значения показателей находятся в промежутке между годами
Суть метода скользящей средней состоит в том, что вычисляется средний уровень из определенного числа первых по порядку уровней ряда, затем – средний уровень из того же числа уровней, начиная со второго, далее – начиная с третьего и т.д. Таким образом, при расчетах среднего уровня как бы «скользят» по ряду динамики от его начала к концу, каждый раз отбрасывая один уровень в начале и добавляя один следующий.
Средняя из нечетного числа уровней относится к середине интервала. Если интервал сглаживания четный, то отнесение средней к определенному времени невозможно, она относится к середине между датами. Для того чтобы правильно отнести среднюю из четного числа уровней, применяется центрирование, т.е. нахождение средней из средней, которую относят уже к определенной дате.
1. Рассчитаем трехлетние скользящие суммы. Пример 4(окончание).
Находим сумму урожайности за 1989–1991 гг.: 19,5 + 23,4 + 25,0 = = 67,9 и записываем это значение в 1991 г. Затем из этой суммы вычитаем значение показателя за 1989 г. и прибавляем показатель за 1992 г.: 67,9 - 19,5 + 22,4 = 70,8 и это значение записываем в 1992 г. и т.д.
2. Определим трехлетние скользящие средних по формуле простой
средней арифметической:

Полученное значение записываем в 1990 г. Затем берем следующую трехлетнюю скользящую сумму и находим трехлетнюю скользящую среднюю: 70,8 : 3 = 23,6, полученное значение записываем в 1991 г. и т.д.
Аналогичным образом рассчитываются четырехлетние скользящие суммы. Их значения представлены в графе 4 таблицы данного примера.
Четырехлетние скользящие средние определяются по формуле простой средней арифметической:

Это значение будет отнесено между двумя годами –1990 и 1991 гг., т.е. в середине интервала сглаживания. Для того чтобы найти четырехлетние скользящие средние центрированные, необходимо найти среднюю из двух смежных скользящих средних:

Эта средняя будет отнесена к 1991 г. Аналогичным образом рассчитываются остальные центрированные средние; их значения записываются в графу 6 таблицы данного примера.
9.1. ПОНЯТИЕ ИНДЕКСОВ. ИХ ВИДЫ
Индексы – важнейший обобщающий показатель. С их помощью можно измерить динамику социально-экономического явления за два или более периодов времени, динамику среднего показателя и сопоставить уровни явления в пространстве, по странам, экономическим районам, областям и т.д. Индексы используются для определения степени влияния изменений значений одних показателей на динамику других, а также для пересчета значений макроэкономических показателей из фактических цен в сопоставимые.
Простейший показатель, применяемый в индексном анализе,– индивидуальный индекс, который характеризует изменение во времени или в пространстве отдельных однородных элементов совокупности. Например, индивидуальные индексы физического объема продукции, цен, себестоимости единицы продукции.
В экономических расчетах чаще всего используются сводные, или общие, индексы, которые характеризуют изменение совокупности в целом.
Построение этих индексов является содержанием индексной методологии, в которой сложились две концепции: синтетическая и аналитическая.
Согласно синтетической концепции особенность общих индексов состоит в том, что они выражают относительное изменение сложных явлений, отдельные части которых непосредственно несоизмеримы, и поэтому индексы – показатели синтетические.
В соответствии с аналитической концепцией индексы трактуются как показатели, необходимые для измерения влияния изменения составных частей, факторов сложного явления на изменение уровня этого явления. Поэтому индексной методологией предусматривается определение влияния каждого из факторов путем элиминирования влияния других факторов на уровень изучаемого явления. Такие индексы – показатели аналитические.
Общие индексы строят для количественных и качественных показателей. В зависимости от цели исследования и наличия исходных данных используют различные формы построения общих индексов: агрегатную или средневзвешенную.
При построении агрегатного индекса необходимо решить проблему выбора весов, при этом руководствуются следующим правилом: если строится индекс количественного показателя, то веса берутся за базисный период; если строится индекс качественного показателя, то используются веса отчетного периода.
В статистической практике, помимо агрегатных, применяются средневзвешенные индексы: среднеарифметический и среднегармонический.
Индексный метод служит также для изучения динамики средних величин и выявления факторов, влияющих на динамику средних. С этой целью исчисляется система взаимосвязанных индексов: переменного, постоянного состава и структурных сдвигов.
Индекс переменного состава представляет собой отношение двух взвешенных средних величин с переменными весами, характеризующими изменение индексируемого (осредняемого) показателя.
Индекс переменного состава (Iпер.с.) для качественных показателей имеет следующий вид:

Величина этого индекса характеризует изменения средневзвешенной средней за счет влияния двух факторов: осредняемого показателя у отдельных единиц совокупности и структуры изучаемой совокупности.
Индекс постоянного состава (Iп.с.) учитывает изменения только индексируемой величины, показывает средний размер изменения изучаемого показателя у единиц совокупности и выглядит следующим образом:

Для расчета индекса постоянного состава можно использовать агрегатную форму индекса:

Индекс структурных сдвигов (Iстрсдв) характеризует влияние изменения структуры изучаемого явления на динамику среднего уровня индексируемого показателя и рассчитывается по формуле

Под структурными изменениями понимается изменение доли отдельных групп единиц совокупности в общей их численности (d). В индексах средних уровней в качестве весов могут быть взяты удельные веса единиц совокупности 
Тогда систему индексов можно записать в таком виде: 
Система взаимосвязанных индексов имеет следующий вид:

При изучении динамики социально-экономических явлений за некоторый интервал времени, включающий в себя более двух периодов времени, используется система индексов: цепные индексы с переменными весами; цепные индексы с постоянными весами, базисные индексы с переменными весами, базисные индексы с постоянными весами.
Для сравнения (сопоставления) показателей в пространстве (по странам, экономическим районам, областям и т.п.) применяются территориальные индексы.
В рыночной экономике особую роль играют индексы цен, которые позволяют оценить динамику цен на товары, измерить инфляцию при макроэкономических исследованиях, пересчитать важнейшие стоимостные показатели системы национальных счетов (СНС) из фактических цен в сопоставимые и др. Для решения различных задач могут быть использованы индексы цен Г. Пааше и Э. Ласпейреса. Весами в индексе Г. Пааше выступает количество продукции текущего периода, а в индексе цен Э. Ласпейреса – количество продукции базисного периода.
Средняя геометрическая из произведения двух агрегатных индексов цен Э. Ласпейреса и Г. Пааше представляет собой индекс цен И. Фишера.
10.1. ПОНЯТИЕ ВЫБОРОЧНОГО МЕТОДА
Выборочный метод – это такое несплошное наблюдение, при котором подлежащие обследованию единицы отбираются в случайном порядке, отобранная часть изучается, а результаты распространяются на всю исходную совокупность.
Совокупность, из которой проводится отбор, называется генеральной (все обобщающие показатели совокупности – генеральными). Совокупность отобранных единиц именуют выборочной, а ее обобщающие показатели – выборочными.
Применяя выборочный метод, обычно используют два вида обобщающих показателей: среднюю величину количественного признака и относительную величину альтернативного признака (долю единиц, обладающую тем или иным признаком).
10.2. ОШИБКИ, ВОЗНИКАЮЩИЕ ПРИ ВЫБОРОЧНОМ НАБЛЮДЕНИИ
Основная задача выборочного наблюдения в экономике состоит в том, чтобы на основе характеристик выборочной совокупности (средней и доли) получить достоверные суждения о показателях средней и доли в генеральной совокупности. При решении этой задачи возникают ошибки двух видов: регистрации и репрезентативности (рис. 10.1). Ошибки репрезентативности присущи только выборочному наблюдению и возникают в силу того, что выборочная совокупность не полностью воспроизводит генеральную.

Рис. 10.1. Виды ошибок при выборочном наблюдении
Степень точности выборочных оценок зависит от величины ошибки репрезентативности. В общем виде ошибка репрезентативности, или предельная ошибка выборки, характеризуется величиной расхождения параметров выборочной и генеральной совокупностей. Так, для средней величины имеем:
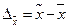 , где
, где
 – предельная ошибка выборки;
– предельная ошибка выборки;  – выборочная средняя;
– выборочная средняя;  – генеральная средняя.
– генеральная средняя.
Величина предельной ошибки выборки, в соответствии с теоремами теории вероятностей, будет кратна средней ошибке:

где t – нормированные отклонения, зависящие от вероятности, с которой гарантируется результат; m– средняя квадратическая стандартная ошибка выборки.
Предельная ошибка выборки позволяет определить предельные значения характеристик генеральной совокупности и их доверительные интервалы:
■ для средней: 
■ для доли: 
Это означает, что с заданной вероятностью можно утверждать, что значение генеральной средней следует ожидать в пределах от  до
до 
Дата добавления: 2014-12-23; просмотров: 1039; Мы поможем в написании вашей работы!; Нарушение авторских прав |