
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
УДК 070(075.8) ББК 76.01я73 С 24 1 страница
| Вид степенной средней | Формула расчета | |
| простая | взвешенная | |
| Арифметическая | 
| 
|
| Гармоническая | 
|  где где  = = 
|
| Геометрическая | 
| 
|
| Квадратическая | 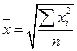
| 
|
| Кубическая | 
| 
|
В интервальном вариационном ряду для расчета средней арифметической взвешенной определяются и используются значения середины интервалов.
Рассмотрим методологию применения разных видов степенных средних на основе расчета средней заработной платы по двум предприятиям вместе: за январь, февраль и за два месяца. Исходные данные представлены в табл. 5.
Таблица 5
| № предприятия | Январь | Февраль | ||
| Средняя заработная плата, руб. | Численность работников, человек | Средняя заработная плата, руб. | Фонд оплаты труда, тыс. руб. | |
| 4 900 | 5 700 | 2 565 | ||
| 5 400 | 5 800 | 3 480 |
Определим исходные соотношения средней для показателя «средняя заработная плата»:

За январь мы располагаем данными о средней заработной плате и численности работников, т.е. нам известен знаменатель исходного соотношения, но неизвестен его числитель. Однако фонд заработной платы можно получить умножением средней заработной платы на численность работников. Поэтому общая средняя может быть рассчитана по формуле средней арифметической взвешенной:
 ,
,
где  -i-й вариант осредняемого признака,
-i-й вариант осредняемого признака,
 -вес i-ого варианта.
-вес i-ого варианта.
За февраль мы имеем только данные о средней заработной плате и фонде оплаты труда, т.е. нам известен числитель исходного соотношения, но неизвестен знаменатель. Численность работников по каждому предприятию можно получить делением фонда оплаты труда на среднюю заработную плату. Тогда средняя заработная плата в целом по двум предприятиям будет рассчитываться по формуле
 ,
,
где  .
.
За два месяца средняя заработная плата по двум предприятиям определяется по формуле средней арифметической простой (невзвешенной), так как веса (f) отсутствуют или равны.
 (руб.),
(руб.),
где n-число единиц или объем совокупности.
Таким образом, исходя из приведенных данных, были применены разные виды степенных средних.
Средняя геометрическая используется в анализе динамики для определения среднего темпа роста.
Средняя квадратическая и степенные средние более высоких порядков используются при расчете ряда статистических показателей, характеризующих вариацию и взаимосвязь.
6. ПОКАЗАТЕЛИ ВАРИАЦИИ
6.1. ПОНЯТИЕ ВАРИАЦИИ. РАСЧЕТ СРЕДНЕГО ЛИНЕЙНОГО ОТКЛОНЕНИ
Различие в индивидуальных значениях признака внутри изучаемой совокупности в статистике называется вариацией признака.
Она возникает в результате того, что его индивидуальные значения складываются под совокупным влиянием разнообразных факторов, которые по-разному сочетаются в каждом отдельном случае.
Средняя величина – это абстрактная, обобщающая характеристика признака изучаемой совокупности, но она не показывает строения совокупности, которое весьма существенно для ее познания. Средняя величина не дает представления о том, как отдельные значения изучаемого признака группируются вокруг средней, сосредоточены они вблизи или значительно отклоняются от нее.
В тех случаях, когда отдельные значения признака близко примыкают к средней арифметической и мало от нее отличаются, средняя хорошо представляет всю совокупность. В тех же случаях, когда отдельные значения совокупности далеко отстают от средней, средняя плохо представляет всю совокупность.
Колебания отдельных значений характеризуют показатели вариации. Однако не всякие различия принято называть вариацией. Под вариацией в статистике понимают такие количественные изменения величины исследуемого признака в пределах однородной совокупности, которые обусловлены перекрещивающимся влиянием различных факторов. Различают случайную и систематическую вариации признака.
Анализ систематической вариации позволяет оценить степень зависимости изменений в изучаемом признаке от определяющих его факторов. Например, изучая силу и характер вариации в выделяемой совокупности, можно оценить, насколько однородной является данная совокупность в количественном, а иногда и качественном отношении, а, следовательно, насколько характерной является исчисленная средняя величина. Степень близости данных отдельных единиц х, к средней измеряется рядом абсолютных, средних и относительных показателей.
Для характеристики совокупностей и исчисленных величин важно знать, какая вариация изучаемого признака скрывается за средним.
Для характеристики колебания признака используется ряд показателей. Наиболее простой из них – размах вариации.
Размах вариации (R) – это разность между наибольшим (хтах) и наименьшим (xmin) значениями вариантов

Пример 1. Имеются следующие данные об объемах товарооборота предприятий.
| Группы предприятий по объему товарооборота, млн руб. | Число предприятий |
| 90-100 | |
| 100-110 | |
| 110-120 | |
| 120-130 | |
| Итого |
Определяем показатель размаха вариации: R = 130 - 90 = 40 (млн руб.).
Этот показатель улавливает только крайние отклонения и не отражает отклонений всех вариантов в ряду.
Для того чтобы дать обобщающую характеристику распределению отклонений, исчисляют среднее линейное отклонение d, которое учитывает различие всех единиц изучаемой совокупности.
Среднее линейное отклонение определяется как средняя арифметическая отклонений индивидуальных значений от средней без учета знака этих отклонений:

Порядок расчета среднего линейного отклонения следующий:
1) по значениям признака исчисляется средняя арифметическая:

2) определяются отклонения каждого вариантах xi, от средней: xi-x;
3) рассчитывается сумма абсолютных величин отклонений: 
4) сумма абсолютных величин отклонений делится на число значений 
Пример 2. Имеются следующие данные о производительности рабочих.
| Табельный номер рабочего | xi-x | |xi-x| | |
| -8 | |||
| -7 | |||
| Итого |
Рассчитаем среднее линейное отклонение:
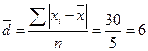
Если данные наблюдения представлены в виде дискретного ряда распределения с частотами, среднее линейное отклонение исчисляется по формуле средней арифметической взвешенной:

Порядок расчета среднего линейного отклонения взвешенного следующий:
1) вычисляется средняя арифметическая взвешенная: 
2) определяются абсолютные отклонения вариантов от средней: 
3) полученные отклонения умножаются на частоты: 
4) находится сумма взвешенных отклонений без учета знака: 
5) сумма взвешенных отклонений делится на сумму частот: 
6 . 2. РАСЧЕТ ДИСПЕРСИИ И СРЕДНЕГО КВАДРАТИЧЕСКОГО ОТКЛОНЕНИЯ ПО ИНДИВИДУАЛЬНЫМ ДАННЫМ И В РЯДАХ РАСПРЕДЕЛЕНИЯ
Основными обобщающими показателями вариации в статистике являются дисперсии и среднее квадратическое отклонение.
Дисперсия – это средняя арифметическая квадратов отклонений каждого значения признака от общей средней. Дисперсия обычно называется средним квадратом отклонений и обозначается а2. В зависимости от исходных данных дисперсия может вычисляться по средней арифметической простой или взвешенной:
 дисперсия невзвешенная (простая);
дисперсия невзвешенная (простая);
 дисперсия взвешенная.
дисперсия взвешенная.
Среднее квадратическое отклонение – это обобщающая характеристика абсолютных размеров вариации признака в совокупности. Выражается оно в тех же единицах измерения, что и признак (в метрах, тоннах, процентах, гектарах и т.д.).
Среднее квадратическое отклонение представляет собой корень квадратный из дисперсии и обозначается 
 среднее квадратическое отклонение невзвешенное
среднее квадратическое отклонение невзвешенное
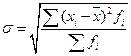 среднее квадратическое отклонение взвешенное.
среднее квадратическое отклонение взвешенное.
Среднее квадратическое отклонение является мерилом надежности средней. Чем меньше среднее квадратическое отклонение, тем лучше средняя арифметическая отражает всю представляемую совокупность.
Вычислению среднего квадратического отклонения предшествует расчет дисперсии.
Порядок расчета дисперсии взвешенной следующий:
1) определяют среднюю арифметическую взвешенную:  ;
;
2) рассчитывают отклонения вариантов от средней: 
3) возводят в квадрат отклонение каждого варианта от средней:  ;
;
4) умножают квадраты отклонений на веса (частоты): 
5) суммируют полученные произведения: 
6) полученную сумму делят на сумму весов: 
Пример 3. Имеются следующие данные о производительности труда рабочих.
| Произведено продукции одним рабочим, шт. (Xj варианта) | Число рабочих, человек
(  ) )
| 
| 
| 
| 
|
| -2 | |||||
| -1 | |||||
| Итого |
Исчислим среднюю арифметическую взвешенную:

Значения отклонений от средней и их квадратов представлены в таблице.
Определим дисперсию: 
Среднее квадратическое отклонение будет равно
 (шт.)
(шт.)
Если исходные данные представлены в виде интервального ряда распределения, то сначала нужно определить дискретное значение признака, а затем применить изложенный метод.
Пример 4. Покажем расчет дисперсии для интервального ряда на данных о распределении посевной площади колхоза по урожайности пшеницы.
| Урожайность пшеницы, ц/га | Посевная площадь, га (  ) )
| 
|  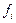
| 
| 
| 
|
| 14-16 | -3,4 | 11,56 | ||||
| 16-18 | -1,4 | 1,96 | ||||
| 18-20 | 0,6 | 0,36 | ||||
| 20-22 | 2,6 | 6,76 | ||||
| Итого |
Средняя арифметическая равна
 (ц/га)
(ц/га)
Вычислим дисперсию:  .
.
6.3. РАСЧЕТ ДИСПЕРСИИ ПО ФОРМУЛЕ ПО ИНДИВИДУАЛЬНЫМ ДАННЫМ И В РЯДАХ РАСПРЕДЕЛЕНИЯ
Техника вычисления дисперсии сложна, а при больших значениях вариантов и частот может быть громоздкой. Расчеты можно упростить, используя свойства дисперсии.
Дисперсия имеет следующие свойства.
1. Уменьшение или увеличение весов (частот) варьирующего признака в определенное число раз дисперсию не изменяет.
2. Уменьшение или увеличение каждого значения признака на одну и ту же постоянную величину А дисперсию не изменяет.
3. Уменьшение или увеличение каждого значения признака в какое-то число раз k соответственно уменьшает или увеличивает дисперсию в k2 раз, а среднее квадратическое отклонение – в k раз.
4. Дисперсия признака относительно произвольной величины(  ) всегда больше дисперсии относительно средней арифметической на квадрат разности между средней и произвольной величинами:
) всегда больше дисперсии относительно средней арифметической на квадрат разности между средней и произвольной величинами:  . Если А = 0, то приходим к следующему равенству:
. Если А = 0, то приходим к следующему равенству:  , т.е. дисперсия признака равна разности между средним квадратом значений признака и квадратом средней.
, т.е. дисперсия признака равна разности между средним квадратом значений признака и квадратом средней.
Каждое свойство при расчете дисперсии может быть применено самостоятельно или в сочетании с другими. Порядок расчета дисперсии простой:
1) определяют среднюю арифметическую: 
2) возводят в квадрат среднюю арифметическую: 
3) возводят в квадрат отклонение каждого варианта ряда: x2i;
4) находят сумму квадратов вариантов:  ;
;
5) делят сумму квадратов вариантов на их число, т.е. определяют средний квадрат: 
6) определяют разность между средним квадратом признака и квадратом средней: 
Пример 5. Имеются следующие данные о производительности труда рабочих.
| Табельный номер рабочего | Произведено продукции, шт. (xi) | xi2 |
| Итого |
Произведем следующие расчеты:
 (шт.)
(шт.)

Рассмотрим расчет дисперсии в интервальном ряду распределения. Порядок расчета дисперсии взвешенной (по формуле  ) следующий:
) следующий:
1) определяют среднюю арифметическую: 
2) возводят в квадрат полученную среднюю:  ;
;
3) возводят в квадрат каждый вариант ряда:  ;
;
4) умножают квадраты вариантов на частоты: 
5) суммируют полученные произведения: 
6) делят полученную сумму на сумму весов и получают средний
квадрат признака: 
7) определяют разность между средним значением квадратов и квадратом средней арифметической, т.е. дисперсию: 
6.4. ПОКАЗАТЕЛИ ОТНОСИТЕЛЬНОГО РАССЕИВАНИЯ
Для характеристики меры изменения изучаемого признака исчисляются показатели изменения в относительных величинах.
Они позволяют сравнивать характер рассеивания в различных распределениях (различные единицы наблюдения одного и того же признака в двух совокупностях, при различных значениях средних, при сравнении разноименных совокупностей). Показатель меры относительного рассеивания рассчитывается как отношение абсолютного показателя рассеивания к средней арифметической, умножаемое на 100%.
1. Коэффициент осцилляции (Ко) отражает относительное изменение крайних значений признака вокруг средней:

2. Относительное линейное отклонение характеризует долю усредненного значения абсолютных отклонений от средней величины:

3. Коэффициент вариации (V):

Поскольку среднеквадратическое отклонение дает обобщающую характеристику изменяемости всех вариантов совокупности, коэффициент вариации является наиболее распространенным показателем колеблемости, используемым для оценки типичности средних величин. Исходят из того, что если V больше 40%, то это говорит о большой колеблемости признака в изучаемой совокупности.
6.5. ПОКАЗАТЕЛИ ХАРАКТЕРИСТИКИ ВАРИАЦИОННЫХ РЯДОВ
Наряду со средней арифметической в статистике применяется средняя гармоническая величина, обратная средней арифметической из обратных значений признака. Как и средняя арифметическая, средняя гармоническая может быть простой и взвешенной.
Характеристиками вариационных рядов наряду со средними являются мода и медиана.
Мода – это величина признака (варианта), наиболее часто повторяющаяся в изучаемой совокупности. Для дискретных рядов распределения модой будет значение варианта с наибольшей частотой.
Для интервальных рядов распределения с равными интервалами мода (Мо) определяется
по формуле

где  начальное значение интервала, содержащего моду
начальное значение интервала, содержащего моду
 – величина модального интервала;
– величина модального интервала;
 – частота модального интервала;
– частота модального интервала;
 – частота интервала, предшествующего модальному;
– частота интервала, предшествующего модальному;
 – частота интервала, следующего за модальным.
– частота интервала, следующего за модальным.
Медиана – это варианта, расположенная в середине вариационного ряда. Если ряд распределения дискретный и имеет нечетное число членов, то медианой будет варианта, находящаяся в середине упорядоченного ряда (упорядоченный ряд – это расположение единиц совокупности в возрастающем или убывающем порядке).
7.1. ПОНЯТИЕ РЯДОВ РАСПРЕДЕЛЕНИЯ
Рядами распределения называются группировки особого вида, при которых по каждому признаку, группе признаков или классу признаков известны численность единиц в группе либо удельный вес этой численности в общем итоге.
Ряды распределения могут быть построены или по количественному, или по атрибутивному признаку. Ряды распределения, построенные по количественному признаку, называются вариационными рядами. Ряд распределения может быть построен по непрерывно варьирующему признаку (признак может принимать любые значения в рамках какого-либо интервала) и по дискретно варьирующему признаку (принимает строго определенные целочисленные значения).
Анализ рядов распределения осуществляется с помощью следующих показателей (показатели центра распределения).
Средняя арифметическая взвешенная (  ):
):  ,
,
где  - середина интервала:
- середина интервала: 
 и
и  – нижняя и верхняя границы интервалов соответственно.
– нижняя и верхняя границы интервалов соответственно.
Медиана (Me) – середина ранжированного ряда.
В интервальном вариационном ряду медиана рассчитывается по формуле  ,
,
где  , – нижняя граница медианного интервала; h- ширина интервала, SMe-1 – накопленная частота интервала, предшествующего медианному, fMe – частота медианного интервала.
, – нижняя граница медианного интервала; h- ширина интервала, SMe-1 – накопленная частота интервала, предшествующего медианному, fMe – частота медианного интервала.
Мода (Мо) – наиболее часто встречающееся значение признака в совокупности.
В интервальном вариационном ряду мода находится в интервале с максимальной частотой и рассчитывается по формуле, которую мы уже приводили:

где  – нижняя граница модального интервала;
– нижняя граница модального интервала;  – частота модального интервала;
– частота модального интервала;  – частота интервала, предшествующего модальному;
– частота интервала, предшествующего модальному;  – частота интервала, следующего за модальным.
– частота интервала, следующего за модальным.
7.2. ПОНЯТИЕ СТАТИСТИЧЕСКИХ ГРАФИКОВ
Большое значение при изучении социально-экономических процессов и явлений имеет графическое изображение статистической информации. Правильно построенный график делает статистическую информацию более выразительной, запоминающейся и удобно воспринимаемой. Графический метод широко применяется для иллюстрации происходящих социально-экономических процессов и явлений.
Применение графиков в статистике насчитывает более чем двухсотлетнюю историю. Основоположником графического метода в статистике коммерческой деятельности считают английского экономиста У. Плейфейра (1731-1798). В своих работах он впервые применил способы графического изображения статистических данных (линейные, столбиковые, секторные и другие диаграммы).
Статистические графики – это одно из самых наглядных средств представления информации.
Статистический график представляет собой чертеж, на котором при помощи условных геометрических фигур изображаются статистические данные. В результате этого получается наглядная характеристика изучаемой статистической совокупности.
Статистический график состоит из следующих основных элементов:
■ поле графика;
■ графический образ;
■ пространственные и масштабные ориентиры;
■ экспликация графика.
Поле графика представляет собой место, на котором график выполняется. Это листы бумаги, географические карты, план местности и т.п. Поле графика характеризуется его форматом (размерами и пропорциями сторон). Размер поля графика зависит от его назначения.
Графический образ – это символические знаки, с помощью которых изображаются статистические данные (линии, точки, прямоугольники, квадраты, круги и т.д.). В качестве графического образа выступают и объемные фигуры. Иногда в графиках используются негеометрические фигуры в виде силуэтов или рисунков предметов.
Пространственные ориентиры определяют размещение графических образов на поле графика. Эти ориентиры задаются координатной сеткой или контурными линиями и делят поле графика на части, соответствующие значениям изучаемых показателей.
Масштабные ориентиры статистического графика придают графическим образам количественную значимость, которая передается с помощью системы масштабных шкал.
Дата добавления: 2014-12-23; просмотров: 280; Мы поможем в написании вашей работы!; Нарушение авторских прав |