Микросостояние одной микрочастицы.

Среди микрочастиц есть составные (атомы, молекулы, атомные ядра) и элементарные. Обсудим свойства элементарных частиц, не имеющих собственных размеров и внутренней структуры. С классической точки зрения они не должны обладать какими-либо другими характеристиками, кроме энергии, импульса, массы и заряда. Однако опыт показал, что это не так. Поясняя это, начнем с обсуждения внутренних характеристик микрочастиц.

По современным данным, например, в электроне нет более «мелких» составных частей, так что с классической точки зрения электрон – точечный объект и характеристики типа собственного момента у него быть не должно. Тем не менее уже довольно давно выяснилось, что многие свойства атомов и особенно их поведение в магнитном поле невозможно объяснить, если считать, что электрон не имеет никаких специфических внутренних характеристик.

Первым, кто это понял, был В. Паули. В 1924 году он показал, что для объяснения различных свойств атомов необходимо предположить, что электрон обладает двузначной внутренней характеристикой, не имеющей классического аналога. Действительно, в классической физике у «точечного» электрона собственный момент должен быть равен нулю, а у «протяженного» электрона с радиусом r»10^-13см величина момента, способная объяснить эксперимент, соответствовала бы линейной скорости на поверхности «вращающегося» электрона, намного превышающей скорость света с.

В этих условиях Дж. Улленбек и С. Гаудсмит (1925г.) высказали смелую гипотезу, согласно которой электрон все же обладает собственным моментом, но имеющим чисто квантовую природу. Они его назвали спином.

Дальнейшее развитие физики показало, что понятие спина, величина которого определяется постоянной Планка, свойственно всем микрочастицам. Оно является для них столь же фундаментальным, как и понятия массы и заряда, и его следует воспринимать как исходное, внутренне присущее им качество.

Для исследования спина электрона и его проекций необходимо, прежде всего, научиться их «выделять» в чистом виде. Здесь решающую роль играет то обстоятельство, что электрон – заряженная микрочастица, так что с его спином неразрывно связан собственный магнитный момент.

Принципиальный опыт такого типа впервые был поставлен О.Штерном и В. Герлахом еще в 1921 году. Они пропускали поток «одинаковых» электронов через сильно неоднородное магнитное поле. Если бы у электронов собственный магнитный момент отсутствовал, магнитное поле не должно было бы оказывать на них влияния. Тем самым, мы здесь сталкиваемся с проявлением качественно новых физических характеристик, которые невозможно истолковать в рамках классической физики. Проекции спина электрона – это характеристики спиновых микросостояний, которые только по размерности совпадают с проекциями момента. Точнее характеристиками спиновых состояний являются спиновые квантовые числа, равные ± .

Иначе говоря, наличие у микрочастиц специфической характеристики – спина, зависящего от постоянной Планку 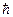, показывает, что электроны и другие элементарные или составные микрообъекты – это особые «квантовые» частицы, или микрочастицы, свойства которых невозможно описать в рамках классического взгляда на природу, так что небольшими поправками к классической физике уже не обойтись. Необходимо перейти к качественно иному, неклассическому, описанию природы.

Впервые такое описание наметилось при изучении свойств электромагнитного излучения, в частности, света. Дело в том, что в классической физике к описанию свойств света успешно применялись обе модели – корпускулярная и волновая. Некоторые свойства света (прямолинейное распространение, отражение и преломление, отклонение в поле тяготения) проще описываются в корпускулярной модели, тогда как другие (интерференция, дифракция, поляризация) в волновой модели. Из классической теории электромагнетизма Максвелла следовало, что свет и другие электромагнитные излучения способны переносить любые, сколь угодно малые доли энергии, импульса и момента. Однако если бы это было в действительности так, мы не могли бы наблюдать удаленные звезды, поскольку плотность переносимой энергии света (или его интенсивность) должна по теории Максвелла убывать обратно пропорционально квадрату расстояния. В этом случае до наблюдателя доходила бы малая доля энергии, которая оказалась бы значительно ниже порога чувствительности любого регистрирующего прибора. Тот факт, что звезды все же наблюдаются, служит прямым указанием на то, что энергия света не всегда зависит от интенсивности волны и поэтому с расстоянием не убывает.

Исследуя свойства света в рамках волновой модели классической физики. В ней электромагнитное излучение представляют в виде совокупности независимых гармонических волн или нормальных мод с определенными значениями w и k. Проверкой того, что подобное описание адекватно физическому объекту, является тот факт, что для электромагнитных волн любого частотного диапазона наблюдаются явления интерференции и дифракции.

Возникает вопрос, наблюдаются ли подобные явления в случае света малой интенсивности, т.е. для небольшого числа одинаковых фотонов. Опыты по пропусканию фотонов вдоль оси достаточно узкой щели показывают, что после щели они регистрируются в пределах области, превышающей размер щели, хотя это не укладывается в рамки волновой модели. Более того, совокупность последовательно зарегистрированных фотонов полностью воспроизводит картину, соответствующую дифракции электромагнитного излучения с частотой w и волновым числом k, несмотря на то, что каждый фотон регистрируется только один раз и притом локально, т.е. в одной точке пространства. Из этого можно сделать как минимум три важных заключения.

Во-первых, локальность регистрации свидетельствует о том, что к фотону в момент регистрации все-таки можно применить модель частицы.

Во-вторых, наблюдаемый эффект колоколообразного распределения числа попаданий одинаковых фотонов в разные участки щели следует приписать неконтролируемому воздействию щели на каждый фотон, которое и вызывает изменение его первоначального состояния.

В-третьих, признаками волны, т.е. способностью к дифракции, следует наделить состояние фотона до щели.

Таким образом, фотон – это материальный объект микромира. Если исходить из идеи единства природы, то аналогичное описание должно быть эффективно и в отношении любых других микрообъектов – электронов, протонов, нейтронов и т.п. Каждому из них, помимо известных из классической физики характеристик – энергии e, импульса р, момента s – необходимо сопоставить и характеристики другого типа, имеющие смысл характеристик его состояния, которые учитывают наличие неконтролируемого воздействия макроскопического окружения. Для свободной микрочастицы с ненулевой массой такими характеристиками являются частота , волновое число (или длина волны де Бройля) l_Бр и спиновые квантовые числа.

Таким образом, после открытия Планка было установлено, что в физической реальности присутствуют две стороны. Это характеристики самого микрообъекта, совпадающие для свободных объектов с аналогичными характеристиками, используемыми в классической физике, и характеристики состояния микрообъекта, учитывающие неконтролируемое влияние макроскопического окружения микрообъекта.

Если микрочастица вынуждена совершать ограниченное движение (как электрон в кристалле или в атоме, атом в молекуле и т.п.), то ее состояние напоминает стоячую волну, представляющую собой суперпозицию двух бегущих в разные стороны волн одинаковой частоты. Длины волн и волновые числа стоячих волн, описывающих микросостояния, зависят от дискретных индексов, которые в этом случай принято называть квантовыми числами. В результате физические характеристики микрообъекта, выраженные через характеристики состояния, также оказываются дискретными, или квантованными. К ним относятся, как правило, энергия, а также импульс или момент. Тем самым, наблюдаемая на опыте дискретность значений физических величин, которые в классической физике были непрерывными, возникает неслучайно. Она отражает фундаментальную роль другой стороны физической реальности – состояния микрообъекта. Квантовые числа – это как раз те самые характеристики состояния, от которых в данных задачах зависят фундаментальные характеристики микрообъектов.

В конечном итоге все многочисленные характеристики, изучаемые в физике ядра и элементарных частиц (изоспин, четность, странность, очарование, цвет) – это квантовые числа, характеризующие эти внутренние состояния микрообъектов.