Ряды распределения.

KurtSchweizer HoldackerstraBe 31 70499 Stuttgart

Телефон: 0711 83631-0 Мобил: 0172 7160501

Факс: 0711 83631-11

E-Mail: kurt.schweizer@metzlergmbh.de Internet: www.metzlergmbh.de

ГЛАВА 9 / 82

Ряды распределения.

План:

1. Ряды распределения и их виды

2. Дискретный (прерывный) ряд распределения и его графическое изображение

3. Интервальный ряд распределения и его графическое изображения.

РЯДЫ РАСПРЕДЕЛЕНИЯ И ЕГО ВИДЫ.

Это статистическая таблица, которая состоит из подлежащего – варианты, х, и сказуемого – частота, m. Вариант – значение изучаемого признака. По виду вариантов ряды бывают:

· Дискретные

· Интервальные

Частота показывает, сколько раз каждый вариант встречается в совокупности.

По данной таблице:

Группы Рабочих по выр-тке (шт) Х	Число Рабочих M	mн	P	Pн	X сер. инт	X*m	X-X	(X-X)m	(X-X)2m	(X-X)3m	(X-X)4m	t = (X-x)4m/ɢ		(t) По табл.	m	Окр. m	m- m	(m- m )2	(m- m )2
А						6=1*5	7=5-253,9	8=7*1	9=7*1	10=7*1	11=7*1	12=9/26,5
180-200			0,015	0,015			-63,9	-191,7	12249,6	-782751,35	50017811,71	-2,401		0,0219	3,306	3,3	-0,3	0,09	0,028
200-220			0,06	0,075			-43,9	-576,8	23125,5	-1015254,228		-1,657		0,1023	15,44	15,4	-0,4	11,56	0,75
220-240			0,25	0,325			-23,9	-1195,0	2856,5	-682595,95		-0,902		0,2661	40,17	40,2	9,8	86,04	2,389
240-260							-3,9					-0,747		0,3951	59,63	59,6	-3,6	12,86	0,217
260-280							16,1					0,608		0,3332	50,29	50,3	-3,3	10,89	0,216
280-300							36,1					1,368		0,1582	23,88	23,9	-0,9	0,81	0,034
300-320							56,1					2,117		0,0431	6,505	6,5	0,5	0,25	0,038
320-340							78,1					2,872		0,0065	0,95	0,95	1,02	1,04	0,6
ИТОГО:										91167,6						200,17			4,8

· Объем совокупности – сумма m = n = 200.

· m_n – накопленная (кумулятивная) частота. Показывает, сколько раз каждый вариант встречается в совокупности, начиная с первого.

· p = m/n – показывает, какой удельный вес занимает каждый вариант во всем объеме совокупности, начиная с первого. Сумма всех долей будет равняться единице (итого).

· p_n = m_n/n – накопленная частость. Показывает, какой удельный вес занимает каждый вариант во всем объеме совокупности, начиная с первого. А в накопленной частости единице равен последний набор.

Гистограмма распределения – это совокупность прямоугольников, основанием которых является длина интервала, а высотой – частота (частость). По оси абсцисс – варианты, по ординат – частоты.

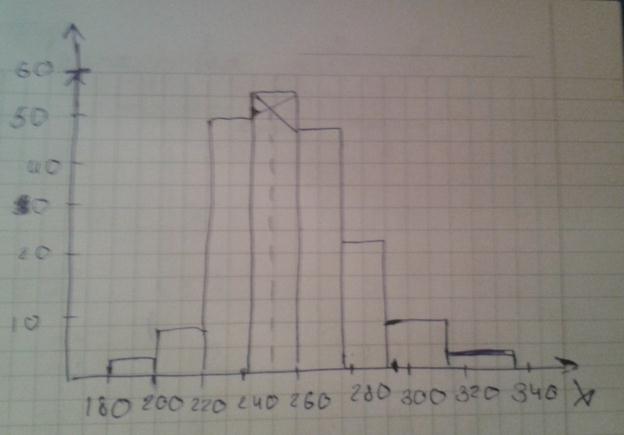
Мода – вариант, который чаще всего встречается в совокупности. Пример: если среди нас большинство 18 лет, то 18 лет – модальный возраст.

Формула: Xm(0) + I ((m2-m1) /(m2-m1) + (m2-m3)),

· где Xm(0) – начало модального i = 240,

· i – интервал = 20,

· m2 – модальная частота = 56,

· m1 – домодальная частота = 50,

· m3 – послемодальная частота = 47.

Мода = 240 + 20 ((56-50) / (56-50) + (56 – 47)) = 248. Модальная выработка у 200 рабочих составляет 248 штук в смену.

Медиана – вариант, который делит распределение пополам. Для того, чтобы графически определить медиану, определяется кумулятор распределение. Она определяется по накопленным частотам (m накопленные). Кумулята начинает строиться с верхней границы первого интервала. Номер медианы в нашем случае: 200/2 = 100. Выработка 100-го рабочего разделит распределение пополам.

Порядок определения медианы:

1. Определяем номер медианы

2. По накопленным частотам и номеру медианы определяем медианы интервал. Интервал медианы: 240-260 (потому что здесь от 66 до 121 рабочих, 100-ый попадает туда)

Формула: Медиана = Xme + i (∑m /2 – Mn (до медианового интервала))/ Mme, где

· Xme = 240

· ∑m = 200

· Mn = 65

· Mme = 56 – количество работников, находящихся в интервале, с которым мы работаем

Медиана = 240 + 20 (200/2 – 65)/56 = 240 + 20 * 35/56 = 240 + 12,5 = 252,5. Вывод: Первая половина рабочих – выработка до 252,2 штук, а вторая половина – после этого числа.

Построение медианы:

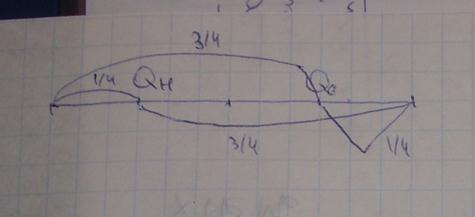
Квартили делят распределение на 4 равные части. Нижняя квартель делит распределение на ¼ к ¾, а квартель верхняя как ¾ к ¼ . Порядок определения:

1. Определяем номер: 1\4 * СУММ м. Выработка 50 рабочего разделит выработку как ¼ к ¾.

2. Квартиль нижняя = х квартиль нижняя + ай * (СУММ м/4 – Мн (до квартильная ай)/М квартильная. Расчет: квартильный интервал: 220-240. 220 + 20 * (50 – 15)/50 = 234. 25% рабочих имеют выработку до 234 штук в смену, а остальные 75% - выше 234.

3. Верхняя квартиль: 150 = ¾ сумм М: 260 + 20*(150 – 121)/47 = 272,34. 75% рабочих имеют выработку до этой величины и 25% - выше.

Середина интервала. (180 + 200)/2 = 190.

Среднеарифметическая величина: СУММ хм / СУММ м = 51750 / 200 = 258,75 штук в смену – средняя выработка 200 рабочих.

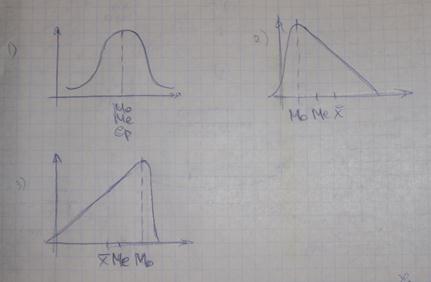
Соотношение моды, медианы и среднего:

1. если мода = медиане и медиана = средней, то будет симметричное распределение или нормальное распределение.

2. Если мода будет меньше медианы,а медиана меньше среднего, то будет правосторонняя ассиметрия.

3. Если наоборот – левосторонняя ассиметрия.

У нас мода = 248, медиана = 252,5 и средняя 253,9 штук. То есть правосторонняя ассиметрия.

Соотношение квартилей и медианы:

1. Если полусумма квартилей = медиане, то будет симметричное распределение

2. Если полусумма квартилей больше медианы – правосторонняя ассиметряя

3. Если полусумма квартилей меньше медианы – левосторонняя ассиметрия

Децели – делят распределение на 10 частей.

· Децель нижняя = х децель нижняя + ай * (СУММ м/10 – Мн (до децельная ай)/М децельная

· Децель верхняя – то же самое, что и верхняя квартиль, только с изменением деления на 10