
КАТЕГОРИИ:
АстрономияБиологияГеографияДругие языкиДругоеИнформатикаИсторияКультураЛитератураЛогикаМатематикаМедицинаМеханикаОбразованиеОхрана трудаПедагогикаПолитикаПравоПсихологияРиторикаСоциологияСпортСтроительствоТехнологияФизикаФилософияФинансыХимияЧерчениеЭкологияЭкономикаЭлектроника
Методические указания. Выборочным наблюдением называется такое наблюдение, при котором обследованию подвергается некоторая часть совокупности
Выборочным наблюдением называется такое наблюдение, при котором обследованию подвергается некоторая часть совокупности, а обобщающие показатели, характеризующие эту исследуемую совокупность, распределяются на всю совокупность в целом.
Проведение выборочного наблюдения обуславливается тремя мотивами:
1.Выборочное наблюдение обладает рядом преимуществ перед сплошным: дает большую экономию сил и средств; значительно экономится время для проведения обследования; представляется возможным значительно расширить программу статистического наблюдения, то есть сделать ее более детальной. К выборочному исследованию статистики прибегают также тогда, когда необходимо уточнить результаты сплошного наблюдения.
2.Когда проводится контроль качества разрушающими методами. Например, испытание деталей (узлов) по прогностным параметрам, в результате которого устанавливаются предельные прочностные показатели, а деталь разрушается.
3.Когда невозможно провести сплошное наблюдение по времени и объему.
Всю массу единиц изучаемого объекта называют генеральной совокупностью. Совокупность единиц, отобранных для выборочного наблюдения, называют выборочной совокупностью.
Обозначим:
N — число единиц, входящих в генеральную совокупность;
п — число единиц, входящих в выборочную совокупность;
 — соответственно средняя величина и дисперсия в выборочной совокупности;
— соответственно средняя величина и дисперсия в выборочной совокупности;
 — соответственно средняя величина и дисперсия в генеральной совокупности;
— соответственно средняя величина и дисперсия в генеральной совокупности;
р — доля признака в генеральной совокупности (генеральная доля);
q — доля единиц, не обладающих определенным признаком (является дополнением генеральной доли до единицы). Сумма обеих долей составляет 1, то есть р + q = 1;
W — отношение числа единиц, обладающих определенным признаком выборочной совокупности, к общей численности выборочной совокупности (выборочная доля).
Рассмотрим пример.
Численность студентов, обучающихся на потоке, составляет 200 человек (табл. 11.1). Определить успеваемость студентов на потоке и долю студентов, имеющих хорошие или отличные оценки, в порядке 20% выборки.
Таблица 11.1
| Оценки (баллы) | Число студентов, чел. |
| Неудовлетворительно (2) | |
| Удовлетворительно (3) | |
| Хорошо (4) | |
| Отлично (5) | |
| Итого: |
Определим по исходным данным генеральной совокупности средний балл студентов по формуле:
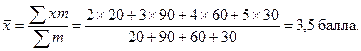
Доля студентов, имеющих хорошие и отличные оценки, составляет:

Осуществим отбор студентов для выборочной совокупности в порядке 20% выборки (табл. 11.2).
Таблица 11.2
| Оценки (баллы) | Число студентов генеральной совокупности, чел. | Число студентов, отобранных в выборочную совокупность, чел. |
| Неудовлетворительно (2) | ||
| Удовлетворительно (3) | ||
| Хорошо (4) | ||
| Отлично (5) | ||
| Итого: |
По отобранным данным выборочной совокупности определим выборочную среднюю  и выборочную долю W. Показатели соответственно составят:
и выборочную долю W. Показатели соответственно составят:


В порядке 20% выборки получили те же самые результаты, что и при использовании данных генеральной совокупности.
В теории выборочного наблюдения есть такое понятие, как ошибка выборки. Ошибкой выборки (ошибкой репрезентативности) называют отклонение выборочных характеристик от генеральных. Ошибка репрезентативности определяется по формулам:

и

Однако о величине данной ошибки можно судить с определенной вероятностью только на основе предельной ошибки выборки:
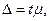
где t — коэффициент доверия, зависящий от вероятности Р, с которой можно гарантировать определенные размеры предельной ошибки.
t = 1 при Р = 0,683;
t = 2 при Р = 0,954;
t = 3 при Р = 0,997;
t = 4 при Р = 0,999.
Рассмотрим пример. Отобрано по жребию 10 рабочих-станочников с дневной выработкой деталей (шт.): 90, 85, 110, 95, 70, 120, 115, 87, 92, 88.
Найдем среднюю выработку  и дисперсию σ2
и дисперсию σ2


Тогда ошибка выборки составит:

или предельная ошибка выборки при t= 2 будет равной

Таким образом, с вероятностью 0,954 можно утверждать, что средняя выработка  шт., находится в пределах:
шт., находится в пределах:

В статистике применяется несколько видов выборки. Вид выборочного наблюдения определяется способом отбора. Из генеральной совокупности можно отбирать единицы в индивидуальном порядке. При индивидуальном отборе выборочная совокупность образуется путем последовательного отбора отдельных единиц. Индивидуальный отбор организуется в порядке случайного отбора, типического и механического. Отбор единиц, проводимый в случайном порядке, называется случайным отбором. Выборка, производимая в порядке индивидуального случайного отбора из генеральной совокупности, называется случайной выборкой.
Отбор единиц из генеральной совокупности, разбитой на однородные типические группы, называется типическим отбором, а выборка, основанная на таком отборе, называется типической выборкой. Отбор единиц из генеральной совокупности может производиться механически через определенный интервал, а выборка в таком случае носит название механической.
Вместе с индивидуальным отбором в статистике имеет место серийный (гнездовой) отбор, когда из генеральной совокупности для выборочного исследования отбираются не отдельные единицы, а целые группы.
Существуют повторный и бесповторный отборы. Отбор называется повторным, если единица или серия, попавшая в выборку, при одном извлечении из жребия не устраняется из дальнейшей жеребьевки, то есть каждый раз жеребьевка производится из всей массы генеральной совокупности. При таком отборе каждая единица может попасть в выборку несколько раз. Повторный отбор еще называют возвратным.
Бесповторным отбором называют такой отбор, при котором один раз отобранная и зарегистрированная единица из отбора устраняется. Повторный и бесповторный отборы производят при проведении случайной, типической и серийной выборок. При механической выборке проводят только бесповторный отбор.
Рассмотрим более подробно каждый вид выборки.
Случайная выборка — отбор единиц производится случайным образом в порядке жеребьевки. Оценка точности случайной выборки осуществляется по следующим формулам (табл. 11.3).
Механическая выборка — отбор единиц из генеральной совокупности проводится механически через интервал, который определяется по формуле 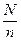 . Механический отбор осуществляется из списка единиц, расположенных в алфавитном порядке, географическом или из ранжированного списка единиц, расположенных в порядке возрастания или убывания. Механическая выборка является более репрезентативной (представительной) по сравнению со случайной, так как дает, как правило, более близкое распределение отобранных единиц к распределению единиц в генеральной совокупности.
. Механический отбор осуществляется из списка единиц, расположенных в алфавитном порядке, географическом или из ранжированного списка единиц, расположенных в порядке возрастания или убывания. Механическая выборка является более репрезентативной (представительной) по сравнению со случайной, так как дает, как правило, более близкое распределение отобранных единиц к распределению единиц в генеральной совокупности.
Таблица 11.3
Дата добавления: 2014-12-23; просмотров: 393; Мы поможем в написании вашей работы!; Нарушение авторских прав |